1
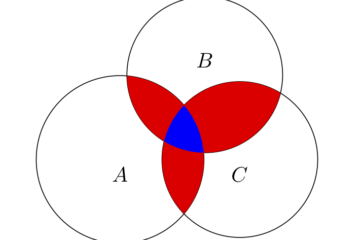
The principle of inclusion-exclusion is an important result of combinatorial calculus which finds applications in various fields, from Number Theory to Probability, Measurement Theory and others. In this article we consider different formulations of the principle, followed by some applications and exercises. For further information, see for example [1] and Read more…
In this article we propose some exercises on Elementary Number Theory; they don’t require advanced mathematical knowledge. Other articles will follow with exercises related to this beautiful branch of mathematics. We recall that the symbol \(\left\lfloor x \right\rfloor\) denotes the integer part of the real number \(x\), i.e. the largest Read more…
Problem Let P be a convex polygon with \(n \) sides. Calculate in how many different ways the polygon can be divided into triangles using diagonals that do not intersect each other in the interior of P. This problem was proposed by Euler in 1751 to his friend Christian Goldbach. Read more…
Problem Suppose we only use the digits of the set \(A = \{1,2,3,4,5 \} \). How many numbers of \(n\) digits can be formed with the set \(A\), if all adjacent digits differ exactly by \(1\)? We denote the number we are looking for with \(a(n) \). HintIf \(n = Read more…
In this article we propose some combinatorial problems related to the chessboard and the game of chess, which have a scope of application in other sectors of Mathematics as well. Exercise 1 We number an \(8 \times 8 \) chessboard with the numbers from \(1\) to \( 64\). Arrange \(8\) Read more…
Problem 1 Let a square lattice of dimensions \(n \times n\) be given.Calculate the number \(R\) of different rectangles which can be drawn, with the vertices in the lattice points.Two rectangles are considered different if they have different sizes or are in different positions. SolutionLet us first consider the case Read more…
Problem 1 Calculate the maximum number of parts in which a plane can be divided by \(n\) lines. Solution 1.1A necessary condition is that the \(n\) lines must intersect two by two and no three lines intersect at the same point. We can proceed by induction: once we draw \(k\) lines, Read more…
Exercise 1 A square and a triangle have the same area. Which shape has the greatest perimeter? HintIt may be useful to remember the following formula: Arithmetic Mean-Geometric Mean InequalityLet \(x_{1},x_{2}, \dots x_{n}\) be non-negative real numbers; then: \[ \dfrac {x_{1}+ x_{2} + \cdots x_{n}}{n} \ge \sqrt[n]{ x_{1}x_{2} \cdots x_{n}} Read more…
Problem Let \((a_{1},a_{2}, \cdots ,a_{n})\) be a permutation of the set \(\{1,2, \cdots,n \}\). Compute the average value, indicated with \(M_{n}\) , of the following sum: \[ (a_{1}- a_{2})^2 + (a_{2}-a_{3})^2 + \cdots + (a_{n-1} – a_{n})^2 \] taken on all permutations. If \(n=2\) the set of permutations is \(\{12,21\}\) Read more…
Euclidean geometry studies geometric objects such as lines, triangles, rectangles, circles, etc. Fractals are also geometric objects; however, they have specific properties that distinguish them and cannot be classified as objects of classical geometry. Although Mandelbrot (1924-2010) is generally considered the father of the scientific theory of fractals, in reality the ideas underlying Read more…