Number of Rectangles in a Square Lattice

Problem 1

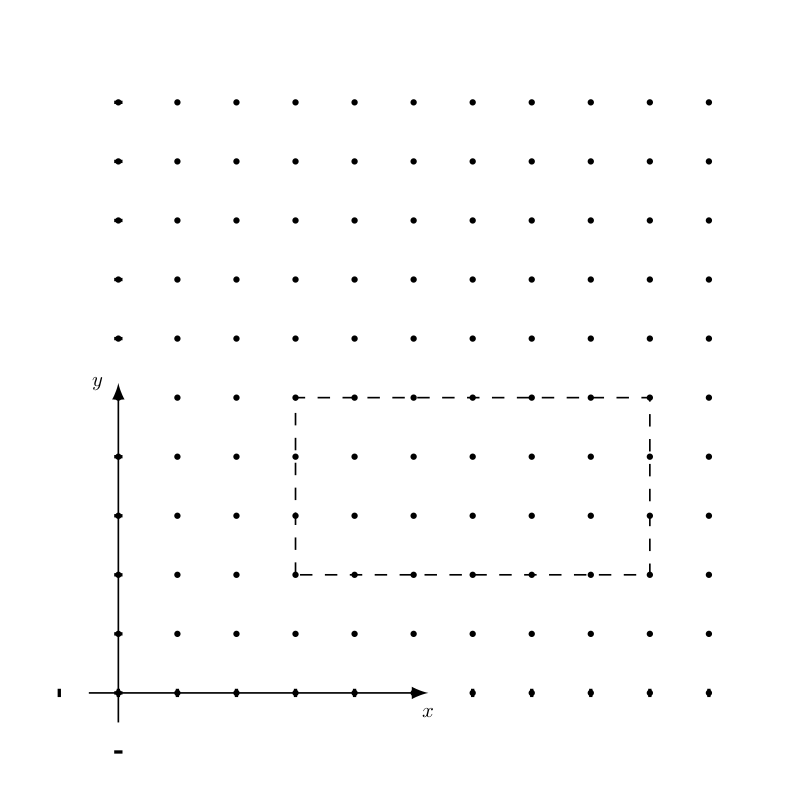
Let a square lattice of dimensions \(n \times n\) be given.
Calculate the number \(R\) of different rectangles which can be drawn, with the vertices in the lattice points.
Two rectangles are considered different if they have different sizes or are in different positions.

Solution
Let us first consider the case of a lattice of \(10\) squares of unit length. Consider a rectangle with the base of \(k\) consecutive squares and height of \(h\) consecutive squares. The group of \(k\) consecutive columns of the base can be chosen in \((11-k)\) different ways. In a similar way the group of \(h\) consecutive lines of the height can be chosen in \((11-h)\) different ways. So the total number of rectangles of size \(k \times h\) is \((11-k) (11-h)\).
Now, the rectangles with a fixed base \(k\) can have height equal to \((1,2, \cdots ,10)\). So in total the number of rectangles with base \(k\) is \((11-k) (1 + 2 + \cdots +10) = 55 (11-k)\).
Similarly the base \(k\) can take on the values \(​​(1,2,\cdots,10)\). So the total number of rectangles is \(55 (1 + 2 + \cdots 10) = 55 \cdot 55 = 3025\).
To solve the general case with a lattice of \(n\) squares, just do the same reasoning. The solution is:

\[ R = \left(\frac {n(n+1)}{2}\right)^2=\displaystyle \sum_{k=1}^n k^{3} \]

---

Problem 2

Let a square lattice of dimensions \(n \times n\) be given.
Determine how many different squares, with vertices in the lattice points, can be drawn.
Two squares are considered different if they have different sizes or are in different positions.

Solution
The total number of squares with sides equal to \(k\) is \((n + 1-k) ^ {2}\). We can use the same reasoning as in the previous problem; we find that the total number of squares is:

\[ R= \displaystyle \sum_{k=1}^n k^{2} =\frac{n(n+1)(2n+1)}{6} \]

---

Problem 3

Let us give a cubic lattice of dimensions \(n \times n \times n\), containing \(n ^ {3}\) unit cubes.
Determine how many different cubes, containing an integer number of unit cubes, can be contained in the lattice.
Two cubes are considered different if they have different sizes or are in different positions.

Solution
We can use the same reasoning as in the previous problems. We find the following formula:

\[ R = \left(\frac {n(n+1)}{2}\right)^2=\displaystyle \sum_{k=1}^n k^{3} \]

As we can see, the result coincides with the number of rectangles that can be drawn in a plane square lattice.
As a useful exercise, try to prove that there is a one-to-one correspondence between the sub-cubes contained in the cubic lattice and the rectangles contained in the square chessboard at the base of the cube itself.