In this article we propose some combinatorial problems related to the chessboard and the game of chess, which have a scope of application in other sectors of Mathematics as well.
Exercise 1
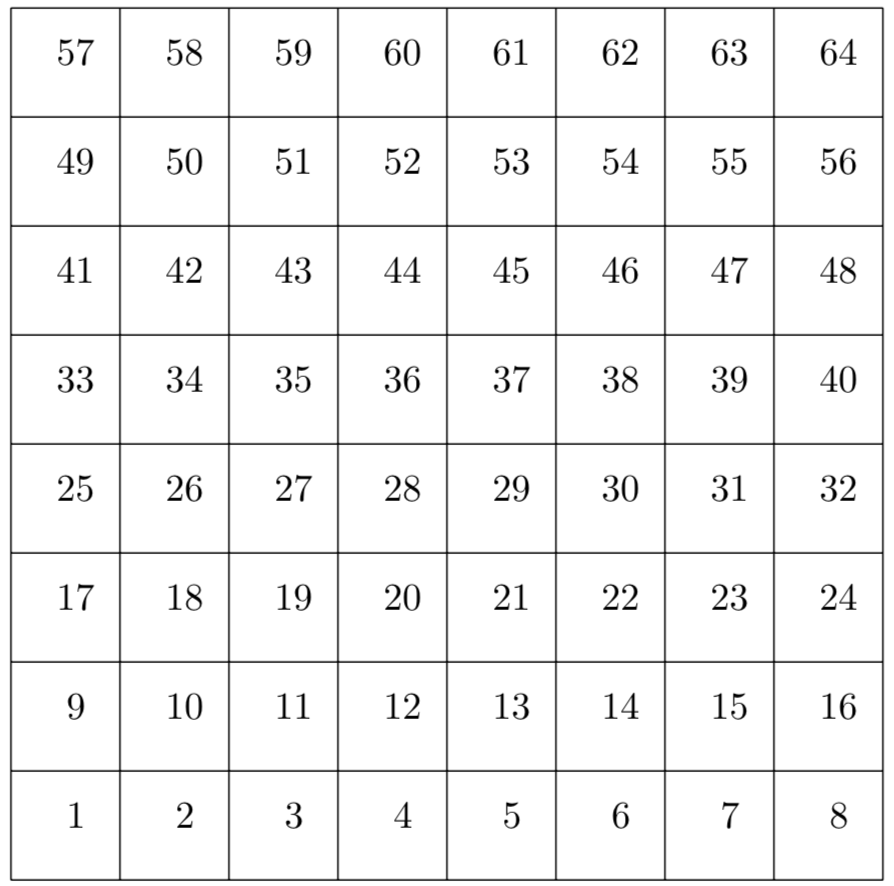
We number an \(8 \times 8 \) chessboard with the numbers from \(1\) to \( 64\). Arrange \(8\) rooks on the chessboard so that none can attack the other. Calculate the sum of the numbers of the squares occupied by the rooks.
Solution
In order for the rooks to not attack each other, in each row and in each column there must be one and only one rook. The element present in the \(i\)-th row and in the \(j\)-th column has the value \(c_{ij} = j+ 8 (i-1)\). However the rooks are arranged, both coefficients \(i, j \) must appear 8 times. So the sum is:
As a generalization, prove that in the case of an \(n \times n \) chessboard and \(n \) rooks arranged so as not to attack each other, the sum is:
\[ S = \frac{n(n^{2} +1)}{2} \]Exercise 2
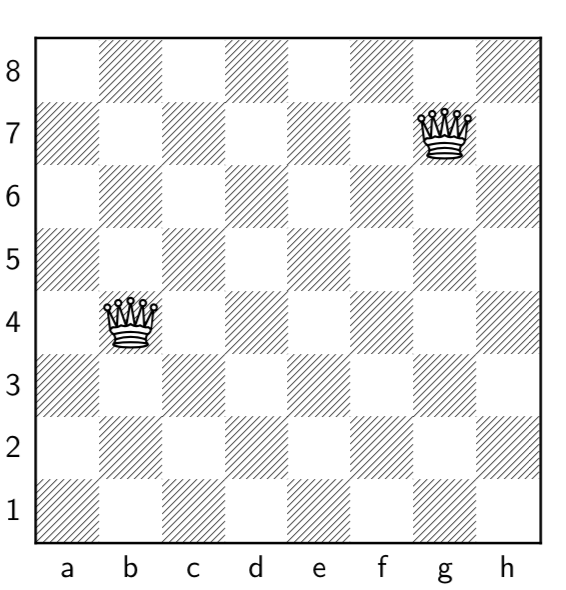
Two queens are randomly placed on an empty chessboard. What is the probability that the two queens cannot attack each other?
Hint
Compute the minimum number of squares that each queen can attack from any position. The apply the principle of composite probabilities.
Solution: [ \(p \approx 0,63\) ]
To learn more about the theory of probability and in particular the principle of composite probabilities see for example [1].
Exercise 3
Determine the greatest number of kings which can be disposed in a way such that none of them lies on a square controlled by another on an \(8 \times 8\) chessboard.
Hint
Divide the chessboard into \(16\) parts, each \(2 \times 2\).
Solution
The maximum number of kings is \(16\).
Exercise 4
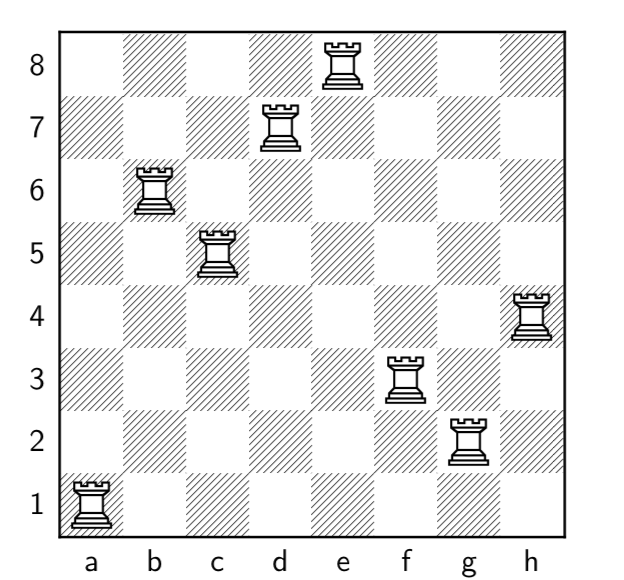
Calculate the maximum number of rooks that can be placed on the \(8 \times 8 \) board, without being able to attack each other.
Solution
It is easily found that the maximum number is \(8 \), as we can se in the chessboard below.
Exercise 5
Suppose we have an \(n \times n \) chessboard. Calculate the number of configurations of \(k \) rooks, with \(k \le n \), such that there are no two rooks on the same row or column.
Solution
Suppose initially that the rooks are distinguishable from each other. In this case, for the first rook we have \(n^{2} \) choices, for the second one the possibilities are \((n-1)^{2} \), and so on. So, the total possible configurations are
where \(D_{n, k} \) indicates the number of dispositions of \(n\) objects taken in groups of \( k\). Since the rooks are not distinct, to solve the problem we have to divide by \(k! \).
We recall the following relationship between the dispositions and the combinations, expressed with the binomial coefficient:
The solution \(r_ {k} \) is therefore given by the following expression:
\[ r_{k} = k!\binom{n}{k}^{2} \\ \]The rook polynomial
The numbers \(r_ {k} \) found in the previous exercise can be used as coefficients of the rook polynomial, defined as follows:
\[ R_{n}(x) = \sum_{k = 0}^{n}k!\binom{n}{k}^{2}x^{k} \]The term rook polynomial was introduced by J. Riordan[2].
The rook polynomial is used to solve combinatorial problems in different areas of Mathematics, outside the topic of chess.
We agree to put \(R_{0} (x) = 1 \). It is also easy to prove that
The meaning is that on an \(1 \times 1 \) chessboard a rook can be arranged in one way only, while zero rooks can be arranged in one way (in the empty chessboard).
To calculate the other polynomials of greater degree we can use the following theorem, which can be proved by using known properties of the binomial coefficients.
Theorem
The rook polynomial satisfies the following recurrence formula:
Exercise 6
Using the formula of the previous theorem, find the expressions for polynomials \(R_{2}(x), R_{3}(x) \)
Solution
\[ \begin{array}{l} R_{2}(x) = 1+4x + 2x^{2} \\ R_{3}(x) = 1+9x+ 18x^{2}+ 6x^{3} \end{array} \]For example, the meaning of the expression \(R_ {2} (x) \) is that on a \(2 \times 2 \) chessboard two rooks can be arranged in two ways, a rook can be arranged in four ways, while zero rooks can be arranged in one way (in the empty board).
It can easily be verified that the first rook polynomials have real, distinct, all negative roots. This is a general property valid for every degree \(n \) of the polynomial, which can be proved by induction using the above recursion formula and Rolle’s theorem of mathematical analysis.
Exercise 7
In how many ways we can arrange \(k\) rooks on an \(m \times n\) chessboard, in a way such that no rook can attack another?
Hint
The proof is similar to that of Exercise 5.
Solution: \(k! \binom{m}{k}\binom{n}{k}\)
APPENDIX – Notes on Laguerre polynomials
The rook polynomials are closely related to the Laguerre polynomials, which have important applications in various areas of Mathematics and Physics. Here are some definitions and properties; for an in-depth study see [3].
Laguerre polynomials can be defined by the following formula:
\[ L_{n}(x) = \sum_{k=0}^{n} \frac {(-1)^{k}}{k!}\binom{n}{k} x^{k} \]It can be shown that they meet the following recursion formula:
\[ (n+1)L_{n+1}(x)=(2n+1-x)L_{n}(x) – n L_{n-1}(x) \]The first Laguerre polynomials are as follows:
\[ \begin{array}{l} L_{0}(x)=1 \\ L_{1}(x)= 1 – x \\ L_{2}(x)= \dfrac{x^{2}-4x+2}{2} \\ L_{3}(x) = \dfrac{-x^{3}+9x^{2}-18x+6}{6} \\ \end{array} \]Bibliography
[1]S. Ross – A First Course in Probability (Pearson)
[2]J. Riordan – An Introduction to Combinatoria Analysis (Wiley)
[3]M. Boas – Mathematical Methods in Physical Sciences (Wiley)

0 Comments