Steiner’s Division of Plane and Space

Problem 1

Calculate the maximum number of parts in which a plane can be divided by \(n\) lines.

Solution 1.1
A necessary condition is that the \(n\) lines must intersect two by two and no three lines intersect at the same point.
We can proceed by induction: once we draw \(k\) lines, we see how a further line increases the number of parts. The \((k + 1)\)-th line must meet each of the \(k\) already drawn lines, obtaining \(k\) distinct intersection points, which divide the added line into \(k + 1\) parts. Thus the \((k + 1)\)-th line cuts exactly \(k + 1\) of the parts into which the plane is already divided: each of these parts is divided into two and therefore the number of parts increases by \(k + 1\).
Let \(R_ {n}\) denotes the maximum number of parts. We can write the following recurrence equation:

\[ R_{n} = R_{n-1} + n \]

with the initial condition \(R_ {2} = 4\).
To solve the equation, we use the tools of finite calculus. First we find the general solution of the homogeneous equation \(R_ {n} – R_ {n-1} = 0\), which in this simple case has a constant solution; then a particular solution is found with the method of undetermined coefficients. 
We try with a second degree polynomial \(p (n) = an ^ {2} + bn + c\). The general solution to the equation is the following:

\[ R_{n}= \frac{n^{2}}{2} + \frac{n}{2}+k \]

where \(k\) is a constant to be determined. Using the initial condition \(R_ {2} = 4\), we find that \(k = 1\) and therefore:

\[ R_{n}= \frac{n^{2}+n+2}{2} \]

To study finite calculus and difference equations see for example ^[1].

Solution 1.2
Let us recall some definitions about the graphs. A graph \(G = (V, A)\) is a pair of sets, where \(V\) is the set of vertices or nodes of the graph, and \(A\) is the set of edges or arcs, each identified by a pair of nodes. The arcs can be oriented or not.
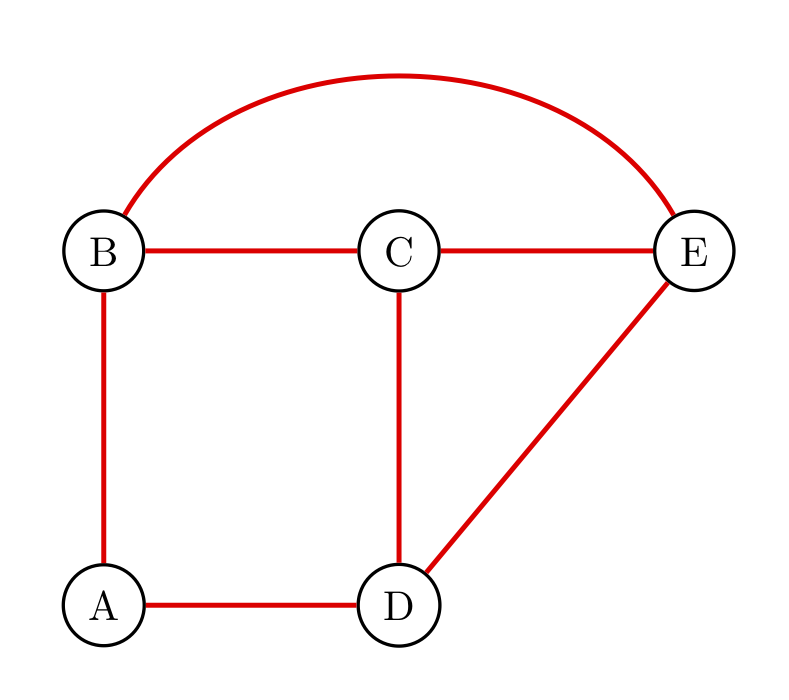
A graph is called planar if at least one graphical representation can be found in which the edges intersect exclusively in the vertices. We call a face or region of the graph every maximal region of the plane bounded between two or more edges, and not further divided into sub areas.  The set of faces also includes the infinite region external to the graph.
For example the following graph is planar with \(5\) nodes, \(7\) arcs and \(4\) faces.

Theorem (Euler Formula) 
Let G be a connected and planar graph. We denote by \(V, E, F\) the number of vertices, arcs and faces. Then the following relationship applies:

\[ V-E+F = 2 \]

For a proof of Euler’s formula, see for example ^[2].
We now use Euler’s formula to solve Problem \(1\). Given the \(n\) lines, we draw a circle that contains all the points of intersection of the lines:

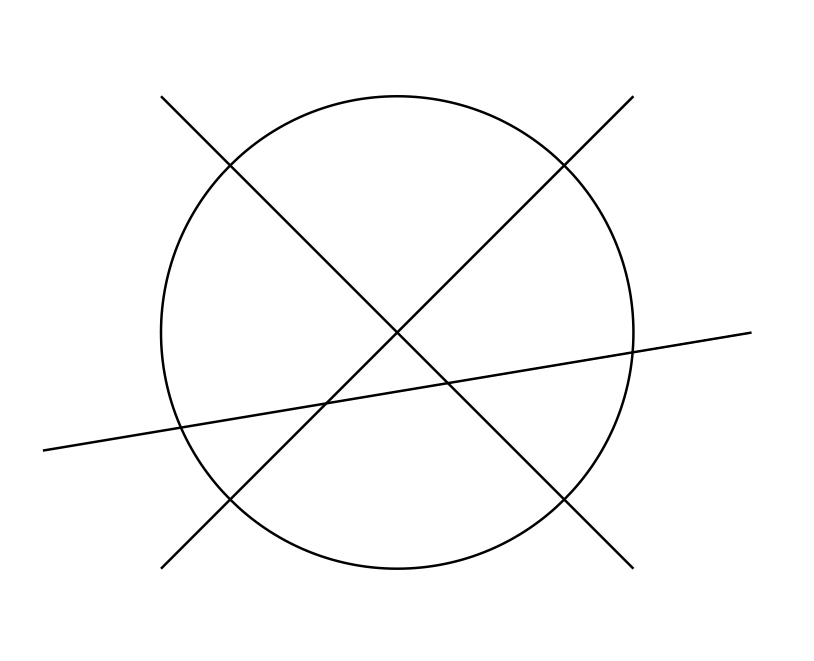
Let us now consider the graph whose nodes are the points of intersection of the lines between them and of the lines with the circle. It is a planar connected graph and therefore we can apply the Euler formula, in the form \(V-E + F = 1\), since we must not consider the region outside the circle.
The number of internal vertices is \(\displaystyle \binom {n} {2}\); the number of external vertices is \(2n\). To calculate the number of arcs, we observe that an external vertex contributes with \(3\), while an internal vertex with \(4\). The total number of arcs is therefore

\[ E = \frac {3 \cdot 2n + 4 \binom{n}{2}}{2} \]

By applying Euler formula we have:

\[ R_{n}= 1 + n +\binom{n}{2} \]

This problem is equivalent to the problem of the maximum number of parts of a pizza that can be made by making \(n\) cuts.

---

Problem 2

Calculate the maximum number of parts in which a plane can be divided by \(n\) circles.

Solution 2.1
As in the previous problem, a necessary condition is that the \(n\) circles intersect two by two and no three circles have a common point. We can proceed by induction in this case as well.
Once drawn \(k\) circles, a new circle intersects all the \(n\) circles and then the circle is subdivided into \(2n\) arcs. Each of these arcs divides in two parts one of the regions that were already present. So the addition of a new circle increases by \(2n\) the number of regions in which the plane is divided.
We denote by \(R_ {n}\) the maximum number of regions into which the plane is divided by \(n\) circles. We can then write the following recurrence equation:

\[ R_ {n} = R_ {n-1} + 2 (n-1) \]

We solve the equation and, taking into account the initial condition \(R_ {2} = 4\), we finally get the solution:

\[ R_{n}= n^{2} – n + 2 \]

Solution 2.2
We create the following circles-vertices-arcs (or circles-nodes-edges) table:

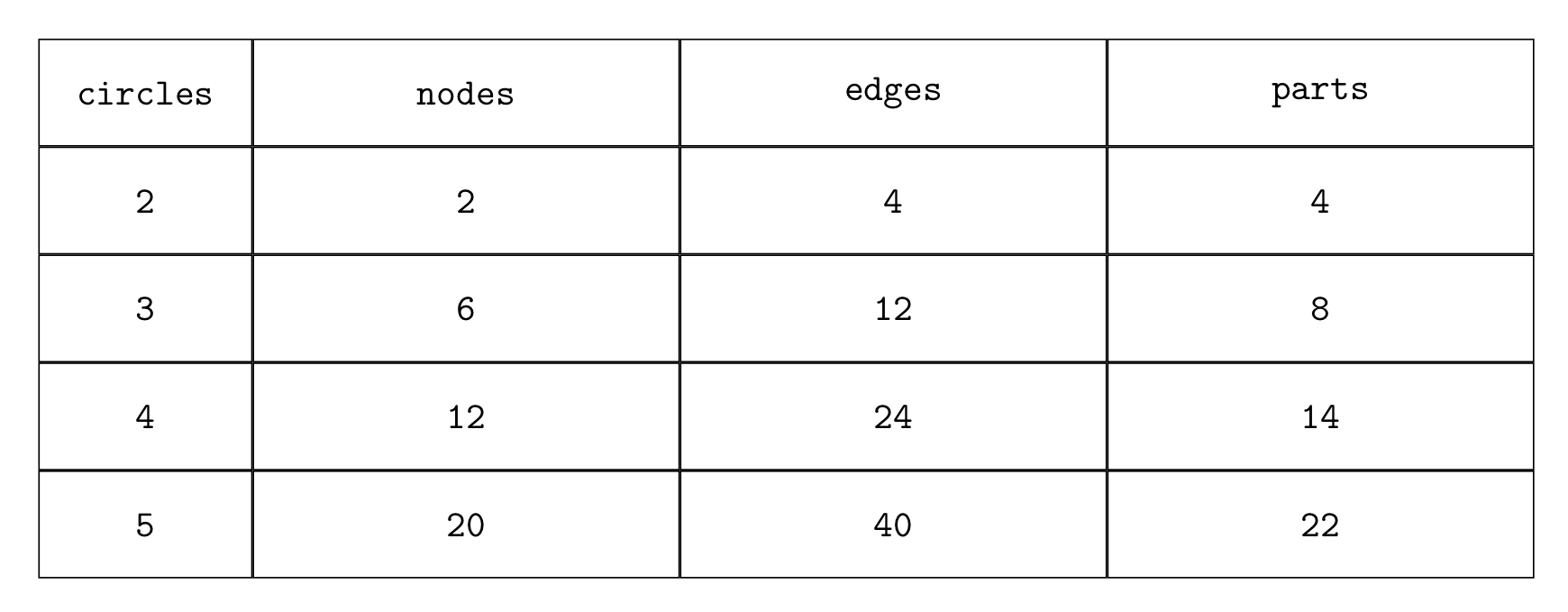
The recurrence equation for vertices is \(V_ {n} – V_ {n-1} = 2 (n-1)\). Solving this equation, taking into account the initial condition \(V_ {2} = 2\), we get \(V_ {n} = n ^ {2} – n\). The number of edges is \(E_ {n} = 2V_ {n}\). Applying the Euler formula \(R_ {n} = E_ {n} -V_ {n} +2\), we get:

\[ R_{n}=n^{2}-n+2 \]

The two previous problems can be generalized in the three-dimensional Euclidean space.

---

Problem 3

Calculate the maximum number of regions in which three-dimensional space can be divided by \(n\) planes.

Solution
Following a reasoning similar to that used for the plane in solution 1.1, we find the following solution:

\[ R_{n}=\frac {n^{3}+5n +6}{6} \]

---

Problem 4

Calculate the maximum number of regions in which three-dimensional space can be divided by \(n\) spheres.

Solution
Following a reasoning similar to that used for the plane in solution 2.1, we find the following solution:

\[ R_{n}=\frac {n^{3}-3n^{2}+8n}{3} \]

For a discussion of Steiner’s problem see for example ^[3] or ^[4].

---

Bibliography

^[1] M. Spiegel; Calculus of Finite differences and difference equations; McGraw-Hill

^[2] A. Tucker; Applied Combinatorics;Wiley

^[3] Knuth, Graham;Concrete Mathematics;Addison Wesley

^[4] L. Comtet; Advanced Combinatorics; D. Reidel