Bertrand Hypothesis and Ramanujan Prime Numbers

The French mathematician Bertrand (1822-1900) formulated the conjecture that for every positive integer \(n\) there is always at least one prime number \(p\) such that

\[ n \lt p \le 2n \]

This conjecture was proved by the Russian mathematician Chebyshev (1821-1894). In this article we will illustrate the proof found by the Hungarian mathematician Erdos (1913-1996), which is based on some properties of the binomial coefficients and does not require the most advanced tools of mathematical analysis. 
At the end, we will mention a very short proof found by the Indian mathematician Ramanujan and we will study a category of prime numbers, introduced by Ramanujan himself, which have interesting properties.

---

1) Introduction

Let us first recall some elementary properties of prime numbers. We introduce the arithmetic function \(\pi (x)\) which counts the number of primes less or equal to \(x\):

\[ \pi(x) = | \{p \in \mathbb{P}: p \le x \}| \]

where \(\mathbb{P}\) is the set of primes \(\{ 2 , 3 , 5 , 7 , ⋯ \}\) and \(x\) is a positive real number.

Theorem 1.1
There are infinite primes. In other words

\[ \lim_{x \to \infty}\pi(x) = \infty \]

There are several proofs on the infinite number of primes, starting with the famous and elegant one of Euclid. Below is a proof based on the properties of the Euler function (see link), which is a multiplicative function. We know that if  \(n=p_1^{a_1}\cdots p_k^{a_k}\) then

\[ \varphi(n)=\prod_{i=1}^k p_i^{a_i-1}(p_i-1) = n \cdot \prod_{i=1}^{k} \left( 1- \frac{1}{p_{i}}\right) \]

Now suppose we have a list of prime numbers  \(p_{1}, \cdots p_{k}\) and let \(n = \prod\limits_{i=1}^{k} p_{i}\) be their product. Then we have

\[ \varphi(n) = \prod_{i=1}^{k} (p_{i}-1) \ge 2^{k-1}\ge 2 \]

as long as \( k \ge 2\). From this inequality we can deduce that there exists an integer in the interval \([2,n]\) which is prime with \(n\), which however has a prime factor distinct from all the \(p_{i}\) of the list.

Theorem 1.2 – Fundamental theorem of arithmetic
Each integer \(n \gt 1\) can be uniquely written in the form

\[ n=p_{1}^{a_{1}}p_{2}^{a_{2}} \cdots p_{k}^{a_{k}}=\prod\limits_{i=1}^{k} p_{i}^{a_{i}} \]

where \(k\) is a positive integer, the \(a_{i}\) are positive integers and \(p_1,p_2,\cdots p_k\) are prime numbers that satisfy the relationship \( p_1 < p_2 < \cdots < p_k\). The proof is found in every elementary text of Number Theory (for example, see ^[1]).

Exercise 1.1
Let \({p_{1},p_{2}, \cdots p_{k}, \cdots }\) be the sequence of prime numbers in ascending order. Prove the following inequality:

\[ p_{n} \lt 2^{2^{n}} \quad \text{ if } n \gt 0 \]

Proof by induction
The statement is true for \(n=1\) as \(p_{1}=2\). Suppose \(p_{n} < 2^{2^{n}}\). Then the integer \(x=p_{1}p_{2} \cdots p_{n}+1\) has a prime divisor other than \(p_{1}, \cdots p_{n}\). Then

\[ p_{n+1} \le x \le 2^{2}2^{2^{2}}2^{2^{3}} \cdots 2^{2^{n}}+1 \lt 2^{2^{n+1}} \]

where we used the geometric sum formula

\[ 1+x + x^{2}+ \cdots + x^{n}=\frac{x^{n+1}-1}{x-1} \]

So the statement is true for every \(n\).

Exercise 1.2
Prove that there are arbitrarily large intervals that are free of prime numbers.

Hint
Just take the numbers in the range \([n!+2,n! +n]\).

---

2) Factorials and their prime factorization

Prime factorization has an important role in proving some theorems regarding the distribution of prime numbers. Recall the factorial definition of a positive integer \(n\)

\[ n! = \begin{cases} n\cdot (n-1)! \quad \text{ if } n \gt 0 \\ 1 \quad \quad \quad \quad \text{if } n=0 \\ \end{cases} \]

Theorem 2.1 – Legendre-de Polignac
The canonical decomposition into prime factors of \(n!\) is

\[ n! = \prod_{p \le n}p^{\alpha (n,p)} \quad \text{ with }\quad \alpha (n,p)= \sum_{i=1}^{r}\Bigl \lfloor \frac{n}{p^{i}} \Bigr \rfloor \]

where the integer is such that \( p^{r} \le n < p^{r+1}\).

Proof
For each prime number we have to calculate the exponent in the prime factorization. Now, the sum

\[ \Bigl \lfloor \frac{n}{p} \Bigr \rfloor + \Bigl \lfloor \frac{n}{p^{2}} \Bigr \rfloor + \cdots \]

contains a finite number of non-null terms. The first term counts multiples of \(p\) , which are the following:

\[ 1 \cdot p, 2 \cdot p, \cdots ,\Bigl\lfloor \frac{n}{p} \Bigr \rfloor \cdot p \]

Some terms of \(n!\) are divisible also by \(p^{2}\) and the number of these is given by the second term. Continuing we have that the sum coincides precisely with the exponent of the prime number in the factorization of \(n!\). Of course, the sum contains only a finite number of non-null terms; in fact, if \(k \gt r\) where \(p^{r} \ge n\), then the term \(\Bigl\lfloor\dfrac{n}{p^{k}}\Bigr\rfloor=0\).

Remark
The largest exponent of a prime in the factoring of an integer is usually indicated with the symbol \(\nu_{p}(n)\). We use the symbol \(\alpha(n,p)\) instead of \(\nu_{p}(n!)\) because it is more convenient in this context.

Exercise 2.1
If \(n=p^{k}\) prove that

\[ \nu_{p} (p^{k}!) = \alpha (p^{k},p)=\frac{n-1}{p-1} \]

Exercise 2.2 (Legendre, 1808)
Let \(n=a_{k}p^{k}+a_{k-1}p^{k-1}+ \cdots + a_{1}p+a_{0}\) be the decomposition of \(n\) according to the base. Prove the following relationship:

\[ \nu_{p}(n!) =\alpha(n,p)=\frac{n-(a_{k}+a_{k-1} + \cdots +a_{0})}{p-1} \]

Hint
Consider the following relationship:

\[ \frac{n}{p^{r}}= a_{k}p^{k-r}+ \cdots + a_{r} + R \]

where \(R\) is a numerical quantity \(\lt 1\) if \(0 \le r \lt k\), since all the digits are less than \(p\), therefore its integer part is equal to zero. From this you can proceed by making slightly laborious but not difficult calculations.

---

3) The binomial coefficients

As is known, the binomial coefficient \(\binom{n}{k}\), where \(n,k\) are positive integers, represents the number of simple combinations of \(n\) objects taken \(k\) at time. Equivalently, it is the number of subsets of order \(k\) which can be made with \(n\) objects. We define \(\binom{n}{0}=1\). The following formulas can easily be proved:

\[ \begin{array}{l} \displaystyle \binom{n}{k}= \frac {n!}{k!(n-k)!} \\ \displaystyle \binom{n}{k}=\binom{n-1}{k} + \binom{n-1}{k-1} \\ \end{array} \]

Binomial coefficients play a fundamental role in many combinatorial problems. Recall for example Newton’s binomial theorem:

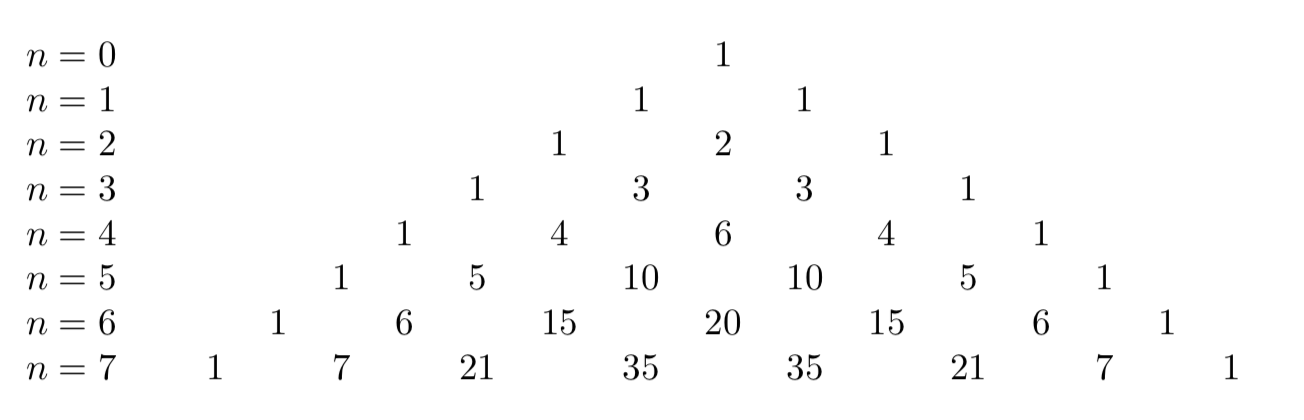
\[ (x+y)^n = \sum_{k=0}^{n}\binom{n}{k} x^{k} y^{n-k} \]

Another important example is the Pascal-Tartaglia triangle:

Each row contains the coefficients of Newton’s binomial expansion of \((a+b)^{n}\). For example, in the row with \(n = 6\) there are the binomial coefficients \(\displaystyle\binom{6}{k}\), with \({k=0,1,2,3,4,5,6 }\).

Exercise 3.1
If \(p\) is a prime number prove that

\[ p | \binom{p}{k} \quad \text {if} \quad 0 \lt k \lt p \]

Exercise 3.2
Prove that 

\[ \sum_{k=0}^{n}(-1)^{k}\binom{n}{k}=0 \]

Exercise 3.3
Prove the following identity:

\[ \sum_{i=0}^{k}\binom{m}{i}\binom{n}{k-i}=\binom{m+n}{k} \]

Hint
Use the following formula:

\[ (1+x)^{m+n} = (1+x)^{m}(1+x)^{n}=\sum_{k=0}^{m+n}\binom{m+n}{k} x^{k} \]

Exercise 3.4
Prove that if \(n\) is odd and \(0 \le k \le n\) then

\[ \binom{n}{k} \le 2^{n-1} \]

Solution

\[ 2^{n}=(1+1)^{n}= \sum_{k=0}^{n}\binom{n}{k}=2 \sum_{k=0}^{\frac{n-1}{2}}\binom{n}{k} \ge 2\binom{n}{k} \]

Exercise 3.5
Prove that the maximum value of the binomial coefficient \(\binom{n}{k}\) is reached with \(k=\dfrac{n}{2}\) if \(n\) is an even number. If it is odd the maximum values ​​are reached with \(k=\dfrac{n-1}{2}\) and \(k=\dfrac{n+1}{2}\).

3.1) Prime factorization of binomial coefficients

The result found for the factorial allows us to find the factorization of the binomial coefficient. Using the formula \(\displaystyle\binom{n}{k}= \dfrac {n!}{k!(n-k)!}\), we find the following expression for the exponent of a prime number in the factorization of the binomial coefficient \( \displaystyle\binom{n}{k}\):

\[ \begin{array}{l} \beta(n,k,p) = \alpha (n,p) – \alpha (k,p) – \alpha (n-k,p) =\\ \sum\limits_{i=1}^{r} \left(\Bigl\lfloor \frac{n}{p^{i}}\Bigr \rfloor – \Bigl\lfloor \frac{k}{p^{i}}\Bigr \rfloor – \Bigl\lfloor \frac{n-k}{p^{i}}\Bigr \rfloor \right) \end{array} \]

Thus, we have the following theorem:

Theorem 3.1
The canonical decomposition of the binomial coefficient \(\displaystyle\binom{n}{k}\) is the following:

\[ \binom{n}{k} = \prod_{p \le n}p^{\beta (n,k,p}) \\ \]

where the integer \(r\) is such that  \( p^{r} \le n < p^{r+1}\).

3.2) The central binomial coefficient

For the proof of Bertrand’s postulate, it is useful to study the properties of the central binomial coefficient \(C_{n}\):

\[ C_{n} = \binom{2n}{n}=\frac{(2n)(2n-1) \cdots (n+2)(n+1)}{n!} \]

In this case, the exponent \(\beta (2n,n,p)\) is simplified:

\[ \begin{array}{l} \beta(2n,n,p) = \alpha (2n,p) -2\alpha (n,p)=\\ \sum\limits_{i=1}^{i=r} \left(\Bigl\lfloor \frac{2n}{p^{i}}\Bigr \rfloor – 2\Bigl\lfloor \frac{n}{p^{i}}\Bigr \rfloor\right) \end{array} \]

where \( p^{r} \le 2n < p^{r+1}\).

Example 3.1
The factorization of \(\binom{120}{60}\) is

\[ \begin{array}{l} \binom{120}{60} = 2^{4} \cdot 3^{2} \cdot 7 \cdot 13 \cdot 17 \cdot 23 \cdot 31 \cdot 37 \cdot 61 \cdot 67 \cdot 71 \cdot \\ \cdot 73 \cdot 79 \cdot 83 \cdot 89 \cdot 97 \cdot 101 \cdot 103 \cdot 107 \cdot 109 \cdot 113 \end{array} \]

Exercise 3.6
Prove that \( \forall x \in \mathbb{R} we have \lfloor 2x \rfloor – 2 \lfloor x \rfloor \in \{0,1 \}\).

Using the previous exercise, we easily obtain an estimate from above of the central binomial coefficient:

Theorem 3.2

\[ C_{n}=\binom {2n}{n} = \prod_{p \le 2n} p^{\beta(2n,n,p)}\le (2n)^{\pi (2n)} \]

An estimate from below is expressed by the following theorem:

Theorem 3.3
For all integers \(n \gt 0\) we have:

\[ C_{n}=\binom {2n}{n} \ge \frac{4^{n}}{2n} \]

Proof

\[ 4^{n}=(1+1)^{2n}=\sum_{k=0}^{2n}\binom{2n}{k}=2+ \sum_{k=1}^{2n-1}\binom{2n}{k} \le 2n \binom{2n}{n} \]

Theorem 3.4
None of the prime powers of the factorization of \(C_{n}\) exceeds \(2n\).

Proof
The exponent relative to a prime factor \(p\) is

\[ \beta (2n,n,p)= \alpha (2n,p) – 2\alpha (n,p) =\sum_{i=1}^{r} \left(\Bigl\lfloor \frac{2n}{p^{i}}\Bigr \rfloor – 2\Bigl\lfloor \frac{n}{p^{i}}\Bigr \rfloor \right) \]

Each term in the summation has a maximum value equal to \(1\). So the summation has value \(\le 2n\), since its terms are all null if \(p^{k} > 2n\).

---

4) The Bertrand postulate

At this point we can complete the last steps necessary to prove Bertrand’s postulate.

Theorem 4.1
If a prime \(p \neq 2\) is such that  \( \dfrac{2n}{3} < p \le n\), then \(p\) does not divide \(C_{n}\).

Proof
If  \( \dfrac{2n}{3} < p \le n\), then \(\lfloor \frac{2n}{p}\rfloor =2 \lfloor \frac{n}{p} \rfloor=2\). If \(n >4\), then \(p^{k} > 2n\) for \( k \ge 2\). The same can be verified for \( n \le 4\). So there are no prime numbers with positive exponents in the interval.

Definition 4.1
Let \((p_{i})\) be the ordered sequence of primes. We call the primorial of \(n\) the following number:

\[ n\# = p_{1} p_{2} \cdots p_{k} \]

where \(p_{k} \le n\) and \(p_{k+1} >n\).

Theorem 4.2
For every positive integer \(n\) we have:

\[ n\# = \prod_{p \le n}p \lt 4^{n} \]

Proof
The theorem is true for \(n=1\) or \(n=2\). Let’s prove it with the induction method. Suppose that it is true for all integers \(k \lt n\) and prove that it is also true for \(k=n\). If \(n\) is not prime then \(n\# = (n-1)\#\) an, for the hypothesis, \(n\# < 4^{n}\). So, suppose that \(n\) is an odd prime \(n=2m+1\). We know that the binomial coefficient

\[ \binom{2m+1}{m}= \frac{(2m+1)!}{m!(m+1)!} \]

is divisible by all prime numbers \(p\) such that \(m+2 \le p \le 2m+1\). Then

\[ \prod_{p \le 2m+1}p \le \binom{2m+1}{m} \prod_{p \le m+1}p \lt \binom{2m+1}{m} 4^{m+1} \]

Now, the two binomial coefficients \(\binom{2m+1}{m}\) and \(\binom{2m+1}{m+1}\) are equal and are present in the binomial expansion of \((1+1)^{2m+1}\). Then

\[ \binom{2m+1}{m} \le \frac{1}{2}2^{2m+1}=4^{m} \]

Putting the results together we finally have

\[ \prod_{p \le 2m+1}p \lt 4^{m}4^{m+1}=4^{2m+1}=4^{n} \]

An alternative form of the previous theorem is the following:

\[ \prod_{p \le x}p \le 4^{x-1} \quad \text{ $\forall x \ge 2$} \]

where \(x\) is a real number. See ^[2].

Now we can complete the proof of Bertrand’s postulate.

Theorem 4.3 – Bertrand postulate
For every positive integer \(n\), there exists a prime number \(p\) such that \(n \lt p \le 2n\).

Proof
Suppose that there is no prime between \(n\) and \(2n\). We know that the prime factors of \(C_{n}\) are all less than or equal to \(\dfrac{2n}{3}\). If \(n \gt 4\) we have the inequality \(\sqrt{2n} < \dfrac {2n}{3}\). We then divide the prime factors of \(C_{n}\) into two groups: those that are less than \(\sqrt{2n}\) with product \(P\) and those that are between \(\sqrt{2n}\) and \(\dfrac{n}{3}\) with product \(Q\); then \(C_{n}=P \cdot Q\). 
The terms of the product \(P\) are all less than \(2n\), then \(P \le (2n)^{\sqrt{2n}}\). The terms of the product \(Q\) have exponents less or equal to \(1\), as it is easy to verify, then \(Q \le (\frac{2n}{3})\#\le 4^{(\frac{2n}{3})}\). Combining with the results we have

\[ \frac{4^{n}}{2n} \le C_{n}=P \cdot Q\le (2n)^{\sqrt{2n}}4^{(\frac{2n}{3})} \]

Simplifying we can write:

\[ 4^{\frac{n}{3}} \le (2n)^{1+ \sqrt{2n}} \]

However, this inequality cannot be true for any value of \(n\). In fact, it can be seen that the left member grows more slowly than the right one as \(n\) increases. It can be shown that the inequality ceases to hold for \(n \ge 468\).
Without exposing the rigorous proof, one can be convinced by analyzing the graph of the function 

\[ f(x)= 4^{\frac{x}{3}}- (2x)^{1+ \sqrt{2x}} \]

for example with the SageMathCell product or with WolframAlpha. In particular, on WolframAlpha you can study the sign of the function by typing the command: ( plot Sign (4^(x / 3) – (2x)^(1+ \ sqrt (2x)))) from x = a to b ). This contradiction implies that the Bertrand postulate is true for at least \(n \gt 467\). However, it can be easily seen that even for lower values ​​the postulate is true. Just find a sequence of prime numbers, each of which is less than double the previous number, for example the following:

\[ 2, 3, 5, 7, 13, 23, 43, 83, 163, 317, 631. \]

---

5) Ramanujan’s proof of the Bertrand postulate

The Indian mathematician Ramanujan (1887-1920), in 1919, presented another elegant and very short proof using more advanced analysis tools, such as Stirling approximation formula. We need to introduce some functions used in the study of the distribution of prime numbers. The function \(\Lambda(n)\)

\[ \Lambda (n)= \begin{cases} \ln p \quad \text{if} \quad n=p^{k} \quad \text{with} \quad k \ge 1 \\ 0 \quad \text{ otherwise} \\ \end{cases} \]

and the functions

\[ \begin{array}{l} \theta (x) = \sum\limits_{p \le x} \ln p \\ \psi (x) = \sum\limits_{n \le x} \Lambda (n) \\ \end{array} \]

The function \(\Lambda(x)\) is called the Mangoldt function in honour to the German mathematician H. Mangoldt (1854-1925). The functions \(\theta(x)\) and \(\psi(x)\) are called Chebyshev functions, in honour to the Russian mathematician P. Chebyshev (1821-1894).

Exercise 5.1
Prove the following formula:

\[ \begin{split} \sum_{d|n} \Lambda (d) = \ln n \\ \end{split} \]

Exercise 5.2

\[ \begin{split} \Lambda (n) = \sum_{d|n} \mu (d) \ln \frac{n}{d} \\ \end{split} \]

Note that \(x^{\frac{1}{k}} < 2\) if \(k > \Big\lfloor \frac{\ln x}{\ln 2}\Big\rfloor\), then \(\theta (x^{\frac{1}{k}})=0\).

We present only some passages from Ramanujan’s proof; for details see ^[3]. The proof begins with the formula

\[ \ln [x]! = \psi(x) + \psi\left(\frac{x}{2}\right)+ \psi\left(\frac{x}{3}\right) + \psi\left(\frac{x}{4}\right) + \cdots \]

From this we derive the following:

\[ \ln [x]! – 2\ln \left[\frac{x}{2}\right]! = \psi(x) -\psi\left(\frac{x}{2}\right) + \psi\left(\frac{x}{3}\right) -\psi\left(\frac{x}{4}\right) \]

We also have

\[ \psi(x) -2\psi (\sqrt{x}) = \theta(x) -\theta(x^{ \frac{1}{2}}) + \theta(x^{\frac{1}{3}}) -\theta(x^{\frac{1}{4}}) + \cdots \]

Since the functions are non-decreasing we have the following relations:

\[ \psi(x) -2\psi (\sqrt{x}) \le \theta(x) \le \psi(x) \] \[ \psi(x) -\psi \left(\frac{1}{2}x\right) \le \ln [x]! -2\ln \left[\frac{x}{2}\right]! \le \psi(x) -\psi\left(\frac{x}{2}\right)+ \psi\left(\frac{x}{3}\right) \]

At this point Ramanujan uses the Stirling formula for the factorial approximation:

\[ \ln n! = n \ln n -n + O(\ln n) \]

where \(O\) is the symbol of Landau (see link). With the Stirling formula he proves the following relationships:

\[ \begin{split} \ln [x]! -2\ln \Big[\frac{x}{2}\Big]! \lt \frac{3}{4}x \quad \text { if } x \gt 0 \\ \ln [x]! -2\ln \Big[\frac{x}{2}\Big]! \gt \frac{2}{3}x \quad \text { if } x \gt 300 \\ \end{split} \]

Using the above formulas with a few steps Ramanujan finally proves the following inequality:

\[ \theta (x) -\theta\left(\frac{x}{2}\right) \gt \frac{1}{6}x -3 \sqrt{x} \quad \text { if } x \gt 300 \]

Since \(\frac{1}{6}x -3 \sqrt{x} \ge 0\) if \( x \ge 324\) the end result is

\[ \theta (2x) -\theta(x) \gt 0 \quad \text {if } x \ge 162 \]

In other words, there is at least a prime number between \(x\) and \(2x\) if \(x >162\). So Bertrand’s postulate is true for \(x \ge 162\). On the other hand, it can easily be verified that it is also true for lower values.

---

6) Ramanujan primes

At the end of his article Ramanujan also proves the following important theorem:

Theorem 6.1

\[ \lim_{x \to \infty} \pi(2x) -\pi(x) = \infty \]

Proof
Based on the function definitions of \(\theta(x)\) and \(\pi(x)\) we have:

\[ \theta(x) -\theta\left(\frac{x}{2}\right) \le \left(\pi(x) -\pi\left(\frac{x}{2}\right)\right) \ln x \]

Using the formula at the end of Ramanujan’s proof, we find the following inequality:

\[ \left(\pi(x) -\pi\left(\frac{x}{2}\right)\right) \gt \frac{1}{\ln x}\left(\frac{x}{6}-3 \sqrt{x}\right) \quad \text { if } x \gt 300 \]

From this, by making simple calculations we can deduce that:

\[ \pi(x) -\pi \left(\frac{x}{2}\right) \ge 1,2,3,4,5, \cdots \quad \text{if } x \ge 2,11,17,29,41, \cdots \]

Definition 6.1
For \( n \ge 1\), the prime number of Ramanujan is defined as the smallest positive integer \(R_{n}\) such that, if  \(x \ge R_{n}\), then

\[ \pi(x) -\pi\left(\frac{x}{2}\right) \ge n \]

We immediately see that \(R_{n}\)  is actually a prime number, due to the minimality condition. The distribution function \(\pi(x)\) must increase at point \(x=R_{n}\). Since the function \(\pi(x)\) can only increase by \(1\) each time, we also have the following relationship

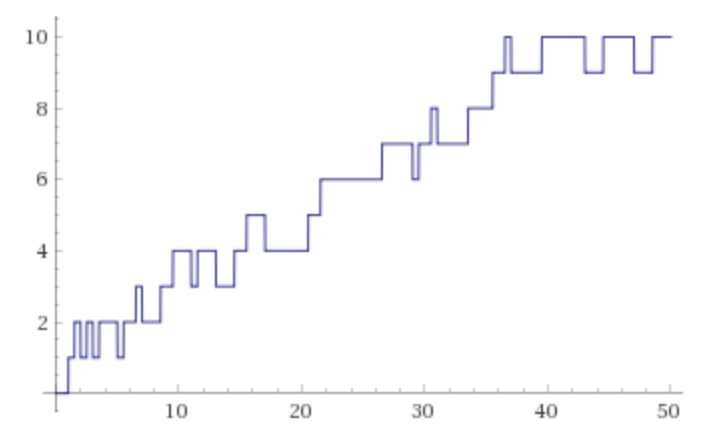
\[ \pi (R_{n}) -\pi({R_{\frac{n}{2}}})=n \]

The function \(f(x)=\pi(x) -\pi(\frac{x}{2})\) is a step function that grows and decreases infinitely many times. Jumps are always \(+1\) or \(-1\) . The graph of the function obtained with the command ( plot PrimePi [2 * x] – PrimePi [x], x from 0 to 5 0 ) on WolframAlpha is as follows:

Bertrand’s postulate is equivalent to \(R_{1}=2\). Some computed values are:

\[ R_{2}=11; R_{3}=17; R_{4}=29;R_{5}=41 \]

Ramanujan’s primes have been studied by important mathematicians. We recall here only some significant properties.

Theorem 6.2
Denote with \(p_{n}\) the \(n\)-th prime number in ascending order. The following relationship holds:

\[ p_{2n} \lt R_{n} \lt p_{3n} \]

For a proof, see the following link.

Theorem 6.3

\[ \lim_{n \to \infty} \frac{R_{n}}{p_{2n}}=1 \]

For an overview of the properties of Ramanujan primes, see ^[4] and also the following link.

---

Conclusion

The proof of Bertrand’s postulate represents an important result in the study of the distribution of prime numbers. In a next article we will describe Chebyshev’s theorems, which will later lead to the proof of the theorem of prime numbers, carried out independently in 1896 by the mathematicians Hadamard and de la Vallée Poussin.

---

Bibliography

^[1]Niven, Zuckerman, Montgomery – An introduction to the Theory of Numbers (V edition, Wiley; p. 20)

^[2]M. Aigner, G. Ziegler – Proofs from THE BOOK (Springer)

^[3]S. Ramanujan – A proof of Bertrand’s postulate (J. Indian Math. Soc. 11, 1919), 181–182

^[4]J. Sondow – Ramanujan primes and Bertrand’s postulate (Amer. Math. Monthly 116, 2009), 630-635