In this short article we will present some problems related to the calculation of points with integer coordinates, contained inside or on the boundary of some plane figures. This type of problem has very interesting aspects and finds important applications in various fields of mathematics.
1) The integer lattice in the plane
A point on the plane \((x,y) \) is called an integer point (or lattice point) if both Cartesian coordinates are integers, that is, if \(x,y \in \mathbb{Z}\). The set of integer points of the plane is called the plane lattice of the integers. We can denote it with the symbol \(\mathbb{Z}^{2}\).
Exercise 1.1
Prove that there cannot exist an equilateral triangle with all three vertices on integer lattice points.
The following theorem also holds:
Theorem 1.1
The only regular polygon in the plane, with all vertices having integer coordinates, is the square.
The proof is not simple (see [1]).
2) The number of integer points contained inside a circle
The following problem was proposed by Steinhaus in 1957 [2].
Problem 2.1 – Steinhaus (1887-1972)
Given a natural number \(n\), check if there is a circle of the plane that contains exactly \(n\) points with integer coordinates in its interior.
We consider two distinct cases:
- Case a – Circle with the center on a point of the lattice.
In this case there are natural numbers \(n\) for which it is not possible to find circles that contain \(n\) integer points. For example, there are no circles that contain \(2,3,4\) integer points. - Case b – Circle with the center in a point that does not belong to the lattice. In this case the following theorem holds:
Theorem 2.1 – Steinhaus
For every natural number \(n\) there is a circle that contains exactly \(n\) points inside.
To prove the theorem we will use the following lemma:
Lemma 2.1
There exists a point of the plane such that all the points of the integer lattice have different distances with the point.
Proof
We define the point \( C\left(\sqrt{u}, \dfrac{1}{v}\right)\) where \(u,v\) are positive integers, \( u \gt 1\) and square-free, and \(v \gt 2\). Suppose that two distinct points of the integer lattice \(P(a,b)\) and \(Q(c,d)\) have the same distance from the point \(C\). Then, applying Euclid’s formula we have:
Taking into account that \(\sqrt{u}\) is an irrational number, it is easy to find that it must be \(a=c\) and \(b=d\), contrary to the assumption that points \(P,Q\) are distinct.
Clearly there is an infinite number of points that you can choose. One example is the point \(C\left(\sqrt{2},\dfrac{1}{3}\right)\), proposed by Sierpinski.
Using the previous lemma, theorem 2.1 is easily proved. We put the integer points of the lattice in ascending order of distance, and stop when we reach the number \(n\) of points.
Note
Steinhaus also proved that for any positive integer \(n\) there exists a circle that has an area equal to \(n\) and contains exactly \(n\) integer points in its interior.
3) Theorem of jacobi
Let us recall an important theorem which is useful for the problem in the next paragraph. We define the arithmetic function \(r_{2}(n)\) as the number of representations of \(n\) in the form
\[ n = x^{2} + y^{2} \ , \quad x,y \in \mathbf{Z} \]We count as different also the representations that differ in a trivial way with respect to the sign or the order. For example, \(r_{2}(1)=4\) because
\[ 1 = (\pm 1)^{2}+ 0^{2}= 0^{2}+(\pm 1)^{2} \]We also define the two arithmetic functions \(d_{1}(n)\) and \(d_{3}(n)\) as the number of divisors of \(n\) of the form \(4k+1\) and \(4k+3\) respectively.
The following theorem was proved by the great mathematician Jacobi (1804-1851) in his important work ‘Fundamenta Nova Theoriae Functionum Ellipticarum’, published in \(1829\).
Theorem 3.1 – Jacobi
\[ r_{2}(n)=4 (d_{1}(n) – d_{3}(n)) \]For a proof see for example [3].
From theorem 3.1 we easily derive the following:
Theorem 3.2
The number of integer solutions of the Diophantine equation
is equal to \(4(t+1)\).
We note that each solution \((A,B)\), with \(A \neq 0, B \neq 0\), gives rise to a group of \(8\) solutions: \((\pm A, \pm B),(\pm B, \pm A)\).
Exercise 3.1
Suppose \(t=2m, m \ge 1\). Prove that the integer solutions of the equation of Theorem 3.2 must be of the following type:
Hint
Note that \(5^{t}=25^{m} \equiv 1 \pmod{8}\).
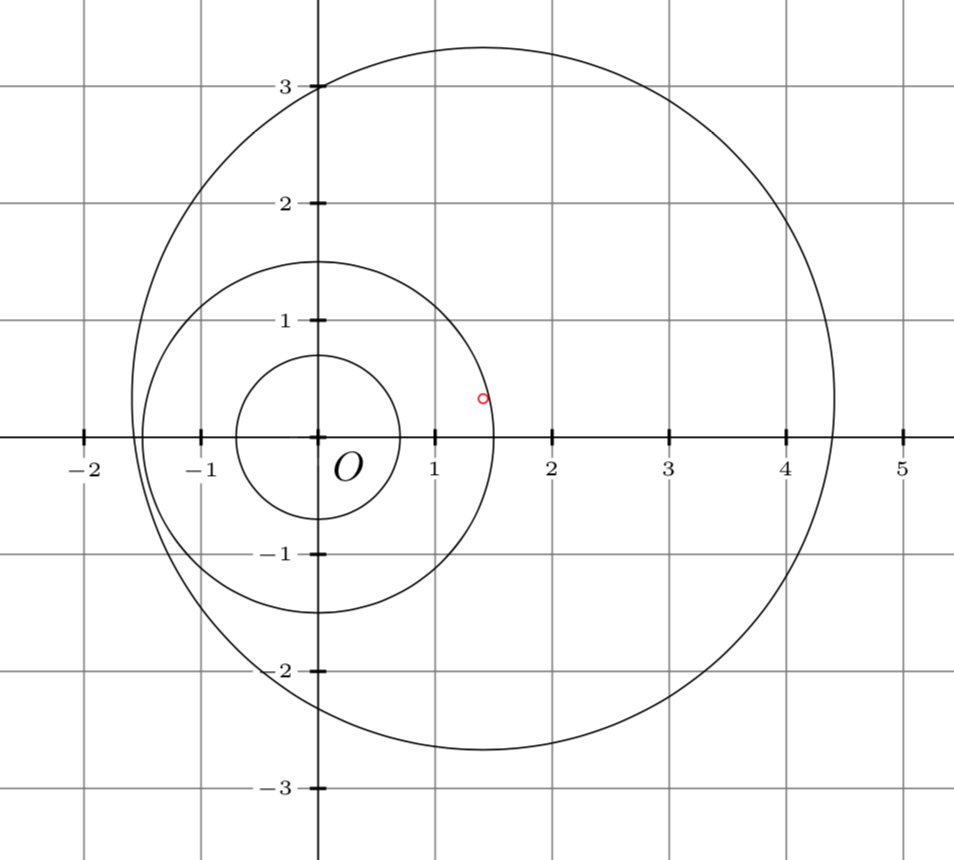
4) Number of integer points contained on the circumference
Problem 4.1
Given a natural number \(n\), verify if there exists a circle of the plane which contains, in its circumference, exactly \(n\) points with integer coordinates.
The answer to the problem is affirmative. In fact, the following theorem was proved by Schinzel [4]:
Theorem 4.1 – Schinzel (1937-2021)
For every \(n \ge 0\), there exists a circle whose circumference crosses exactly \(n\) integer points.
Proof
Suppose first \(n\) even; we set \(n=2(t+1)\). Let us consider the following circle
The number of integer solutions of this equation is half of the total number given by Theorem 3.2 (this is the case in which the first term is odd and the second is even), therefore it is \(2(t+1)=n\).
Now, suppose that \(n\) is odd, with \(n=2m+1\) and \(t=2m\). The equation of the circle to consider is the following:
The number of integer solutions of this equation is equal to the number of solutions \((X,Y)\) of the equation of Theorem 3.2, which satisfy the constraint \(X \equiv -1 \pmod{4}\). According to Exercise 3.1, these solutions are a quarter of the total, in the case \((X \neq 0; Y \neq 0)\). We must add to these the solution \((-5^{m},0)\). Putting together, we have that the total number of integer solutions of the circle is:
\[ 1 + \frac{4(t+1)-4}{4}=t+1=n \]In his article, Schinzel presented the following equations of two circles that satisfy the theorem, in the even and odd cases respectively:
\[ \begin{split} \left(x – \frac{1}{2}\right)^{2}+ y^{2}&=\frac{1}{4}5^{t-1} \quad \text{ n=2t} \\ \left(x – \frac{1}{3} \right)^{2}+ y^{2}&=\frac{1}{9}5^{2t} \quad \text{ n=2t+1} \\ \end{split} \]5) The case of the square
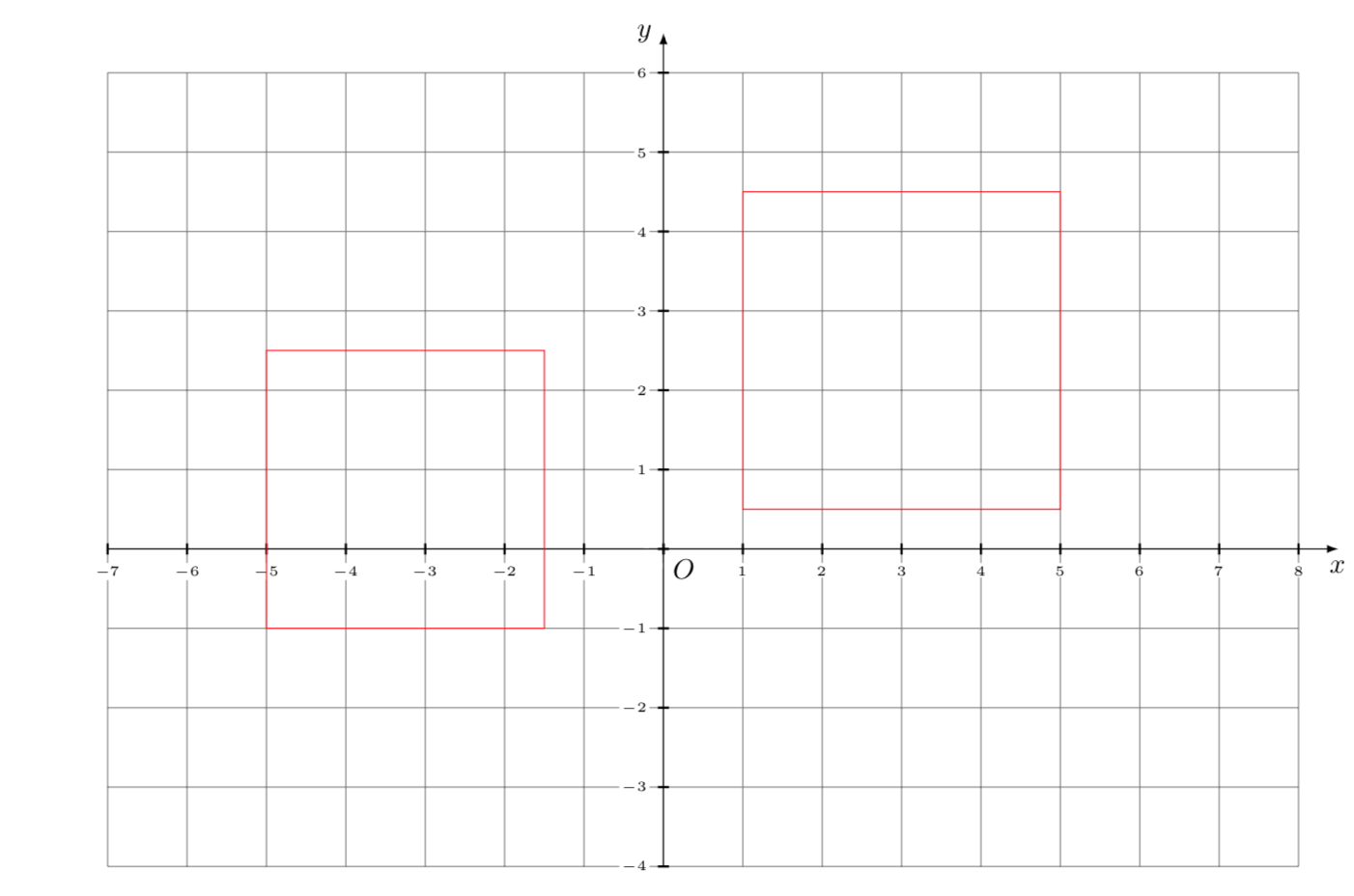
For the square, there is a theorem analogous to that of Steinhaus:
Theorem 5.1
For every natural number \(n\) there exists a square which contains, in its interior, exactly \(n\) points of the lattice of integers.
For a proof, see for example [5].
The case of integer points on the border is easy. We propose it as an exercise.
Exercise 5.1
Prove that, for every natural number \(n\), there exists a square in the plane that has exactly \(n\) integer points on its boundary.
Conclusion
In this article we have limited the study to the plane lattice. It is natural to extend the study to the three-dimensional space, and to determine the number of integer points contained inside or on the surface of three-dimensional geometric figures: sphere, cube, pyramid, etc.
In a future article we will study the two classic problems of the Gaussian circle and Dirichlet’s hyperbola, which play an important role in number theory.
Bibliography
[1]D. Klobučar – On nonexistence of an integer regular polygon (Mathematical Communications, 3 (1), 143-146, 1998)
[2]H. Steinhaus – One Hundred Problems in Elementary Mathematics (Dover Publications Inc., New York, 1964)
[3]Hardy, Wright – An introduction to the Theory of Numbers (V edition – Oxford, 1979)
[4]Schinzel – Sur l’existence d’un cercle passant par un nombre donne de points aux coordonneesentieres (L’Enseiqnement Math. (2) 4, 1958)
[5]Sierpinski – Sur quelques problemes concernant les points aux coordonnees entieres (L’Einseignement Math. (2) 4, 1958, 25-31)

0 Comments