1
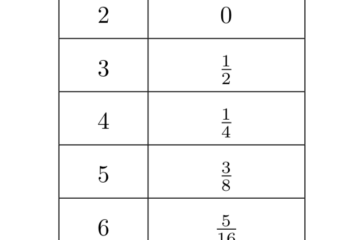
Problem There are four people A, B, C, D. A box with a red ball inside it is given to A, who can leave things unchanged with probability \(p\) or replace the red ball with a white one with probability \(q=1-p\). The box is passed to B who can leave Read more…
1) Gauss’s Modular Arithmetic Given a positive integer \(m \), we say that two integers \( a\) and \(b \) are congruent modulo \(m\) if they give the same remainder when divided by \(m \). We use the following notation introduced by the German mathematician Gauss: \[ a \equiv b Read more…
The study of integers and their properties is the fundamental object of Number Theory. The properties of prime numbers and divisors of an integer were first studied extensively during the period of ancient Greece (Pythagoras, Euclid, etc.); the study resumed again in the seventeenth century, in particular thanks to the Read more…
Problem Suppose we have \( n \) numbers \(x_{1},x_{2}, \cdots x_{n} \), in that order. Compute the number \(C_{n} \) of ways of positioning the brackets to multiply the product of the \(n\) numbers, without changing the given order. HintIf \(n=2\) we have only one case: \((x_{1} x_{2})\) If \(n=3\) Read more…
Problem Suppose we compose numbers using only the digits in the set \( \{1,2,3\}\). Compute the total numbers with the following properties: having length \(n\) beginning and ending with the digit \(\displaystyle 1\) the adjacent digits are always different from each other We indicate this number with \(Z_{n}\). For example Read more…
Problem Let’s consider the following \(5 \times 5\) matrix of positive integers: \[ \begin{pmatrix} d & 2d & 3d & ? & 5d \\ 11 & ? & ? & ? & ? \\ ? & 32 & ? & ? & ? \\ ? & ? & ? & Read more…
A prime number is an integer greater than 1 which is divisible only by 1 and by itself. An integer that is not prime is called composite. Each integer greater than 1 is divisible by at least one prime number. The study of integers and their properties began with the Greeks (Pythagoras, Euclid,…), Read more…