A prime number is an integer greater than 1 which is divisible only by 1 and by itself. An integer that is not prime is called composite. Each integer greater than 1 is divisible by at least one prime number. The study of integers and their properties began with the Greeks (Pythagoras, Euclid,…), and their important results are contained in ‘Euclid’s Elements‘, the most famous mathematical work of classical antiquity.
The Theory of Numbers is the branch of mathematics that studies the properties of prime numbers and integers. The importance and beauty of Number Theory is effectively represented by these words pronounced by Gauss, also referred to as the “Prince of mathematicians” (1777-1855): “Mathematics is the queen of the sciences, and the theory of numbers is the queen of mathematics” Gauss played a fundamental role in the development of number theory. In his work ‘Disquisitiones arithmeticae‘[1], written in Latin and later translated into the main languages, he systematically summarized the results of the previous periods, introduced the modern notations, and exposed a series of results and problems that have addressed the study for mathematicians in the following decades.
A fundamental work for the study of the history of the theory of numbers starting from antiquity is the publication in three volumes by Dickson[2]. For an interesting overview of the current state of Number Theory see Jay Goldman’s book[3].
This article is a quick overview of some of the most significant results regarding Number Theory.
1) Fundamental theorem of Arithmetics
Every integer \(n > 1\) can be written uniquely in the form
\[ n=p_1^{a_1}p_2^{a_2}p_3^{a_3}…p_k^{a_k} \]where \( k \) is a positive integer, \( a_{j} \) is a positive integer and \( \{p_{1},p_{2},\cdots , p_{k}\} \) are prime numbers that satisfy the relationship \( p_{1} < p_{2} < \cdots < p_{k} \). The proof is found in every elementary text of Number Theory[4].
The validity of the theorem may seem obvious at first sight. However, there are many other sets of numbers on which the multiplication operation is defined, with the associative and commutative property, for which the uniqueness of the factorization is not valid. A classic example is that provided by the German mathematician David Hilbert (1862-1943); the numbers belonging to the Hilbert set are the natural ones of the type \( 4n+1, n\in \mathbb{N} \), i.e. the following numbers:
Each Hilbert number is prime or is the product of prime numbers (Hilbert primes do not coincide with the normal primes; for example, 21 is a Hilbert prime).
Exercise 1.1
Prove, by providing at least one example, that the factorization of Hilbert numbers is not unique.
2) The set of prime numbers is infinite
We begin with the proof found in the Elements of Euclid. Assume by contradiction that only \( n \) prime numbers \( p_1, p_2, …,p_n \) exist, with \( n \) a positive integer. We define the integer
\[ Q=p_1p_2 \cdots p_n+1 \\ \]Like every integer, \( Q \) has at least one prime divisor, indicated with \( q \). Now let’s assume that \( q=p_i \) for some \( 1\le i\le n \). Then the number \( q \) would divide the number \( p_1p_2 \cdots p_n \) and also the difference \( Q-p_1p_2 \cdots p_n \). This would imply that \( q \) divides \( 1 \), which is clearly not possible.
There are several different proofs of the theorem. As an example we give the proof of Stieltjes (1890): let there be any finite set of prime numbers \( p_{1}, p_{2}, \cdots {p_k} \) whose product is \( x = p_{1}p_{2} \cdots p_{k} \). Let \( a \cdot b \) be any factorization of the product with distinct \( p_{i} \), that is \( x=a \cdot b \). Then each of the numbers \( p_{i} \) divide \( a \) or \( b \), but not both. So none of the \( p_{i} \) divides the sum \( a+b \) . So there must be at least another number to add to the original set.
3) Sieve of Eratosthenes
Two fundamental problems in number theory are the following:
- factorization: given a positive integer n, find its prime factor decomposition
- primality testing: given a positive integer n, recognize if it is a prime number
The importance of these problems has been emphasized by Gauss in his fundamental work with the following words:”The problem of distinguishing prime numbers from composite numbers and of resolving the latter into their prime factors is known to be one of the most important and useful in arithmetic.”[5]
The sieve of Eratosthenes is a simple and effective algorithm devised by the Greek mathematician Eratosthenes (276 – 194 BC) to identify all the prime numbers lesser than a fixed positive integer.
First we note that the number \( 2 \) is prime (the only even prime number). Then we perform the following steps:
- write the list of all integers greater than 1 up to the largest number n that we want to check;
- remove from the list all the multiples of the first number (the first time will be the multiples of 2). The first number left in the list is a prime number;
- repeat the previous step until there are no more multiples of the prime numbers than are less than n.
In reality the algorithm can be limited to eliminating the multiples lesser than \( \sqrt{n} \) since it is easy to prove that if \( n \) is a composite number, then it has a prime factor that does not exceed \( \sqrt{n} \). In fact if \( n \) is composite then \( n=ab \), where \( a, b \) are integers such that \( 2 \le a,b \), with \( a \le b \). If it were \( a > \sqrt{n} \), then \( \sqrt{n} < a \le b \) and as a result \( ab > n \).
The Eratosthenes algorithm is simple and easy to implement with a computer program; however, for very large values of n it becomes inefficient, even with the most powerful computers. Nowadays the possibility of using more and more powerful computers and the development of new very sophisticated algorithms allow to factor integer numbers with many digits (\( > 100 \)).
4) Prime number theorem
The distribution of prime numbers has been the subject of study by mathematicians since ancient times. The fundamental theorem, glimpsed by Legendre and Gauss, was proved almost simultaneously in 1896 by the mathematicians Hadamard and de la Vallée Poussin. We indicate with \( \pi(n) \) the number of prime numbers \( \le n \). Then the following theorem holds:
\[ \lim_{n\to\infty}\frac{\pi(n)}{n/\log(n)}=1 \]where \( \log(n) \) is the natural logarithm of \( n \). The proof of this theorem is quite complex.
The great Norwegian mathematician Abel defined this as the most important theorem of all mathematics. For an “elementary” proof see Hardy-Wright’s book[6], while for a proof that uses the methods of complex analysis see Apostol’s one[7].
The distribution of prime numbers is extremely irregular. For example, there are arbitrary large gaps in the sequence of primes. Indeed the following theorem is true:
Theorem 4.1
For any positive integer \( n \), there exist \( n \) composite consecutive positive integers.
To prove it, consider the sequence of positive integers:
\[ (n + 1)! + 2, (n + 1)! + 3, …, (n + 1)! + n, (n + 1)! + n + 1 \]Each of these integers is a composite number because \( k \) divides \( (n+1)!+k \) if \( 2\leq k\leq n+1 \).
5) Riemann zeta function and Euler formula
Euler (1707-1783) was one of the greatest mathematicians of all time and made fundamental contributions in many areas of mathematics, particularly in number theory. An important formula discovered and proved by Euler is the following:
\[ \sum_{n=1}^\infty \frac{1}{n^2}=\frac{\pi^2}{6} \\ \]In addition to the intrinsic beauty of this formula, we note the mysterious role of the number \( \pi \), irrational and transcendent, which is the sum of a series computed on the inverse of powers of integers. The function
\[ \zeta(s) = \sum\limits_{n=1}^\infty\frac{1}{n^s} = 1+\frac{1}{2^s}+\frac{1}{3^s}+\frac{1}{4^s}+\frac{1}{5^s}+ \ldots \\ \]where s is a real or complex number, is the famous Riemann zeta function, which plays an important role in many fields of Mathematics, and especially in Number Theory. The connection with prime numbers is given by the following Euler Formula:
\[ \sum_{n=1}^\infty\frac{1}{n^s} = \prod_{p \text{ prime}} \frac{1}{1-p^{-s}} \]where the product extends over every prime number \( p \).
6) Riemann’s hypothesis
The German mathematician Bernhard Riemann (1826-1866), despite his short life, made important and revolutionary contributions in many fields of mathematics. His results on Riemannian Differential Geometry were fundamental for a new conception of the geometry of physical space and for the development of the General Theory of Relativity by Albert Einstein. In the field of Number Theory, Riemann’s main work is represented by his short but very important article published in 1859: “Ueber die Anzahl der Primzahlen unter einer gegebenen Grosse” (On the number of prime numbers below a certain size).
In his study Riemann examines the properties of the zeta function
extending the definition to complex values of the variable s . This function is analytical on the whole complex plane, with the exception of the point \( s=1 \) .
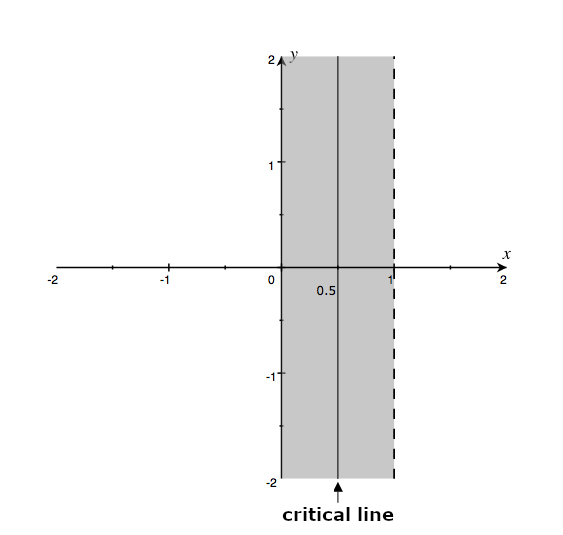
The zeta function has no zeros in the region where the real part of \( s \) is greater than or equal to \( 1 \). In the region where the real part of \( s \) is less than or equal to zero, the zeta function takes the value zero in even negative integers \( \{-2,-4,-6,…\} \); these zeros are called trivial zeros. All remaining zeros are in the strip where the real part of \( s \) \( \in [0,1] \) (the so-called critical strip). It has been shown that there are infinite zeros in the strip on the line \( s=1/2+iy \) where \( y \) takes on real values; this line is called the critical line. Riemann’s hypothesis states that all non-trivial zeros of the zeta function lie on the critical line. To date, all non-trivial zeros have been found on the critical line. Through computers, checks were made on a very large number of zeros. However, Riemann’s conjecture remains one of the most difficult and unsolved problems of mathematics. For an in-depth study of the zeta function and Riemann’s hypothesis see the publications by Edwards[8] and Titchmarsh[9].
7) The Goldbach conjecture
The conjecture was proposed in 1742 by Christian Goldbach (1690-1764) to Euler. There are two versions of the conjecture. Goldbach’s strong conjecture states that every even number greater than 2 is the sum of 2 prime numbers. The weak conjecture states that every odd number greater than 5 is the sum of 3 prime numbers. The strong conjecture implies the weak one but not vice versa. Examples: \( 30 = 17 + 13; 33 = 3 + 17 + 13 \).
At present the conjecture has not been proved, but important progress has been made. The Russian mathematician Schnirelmann (1930) proved the following theorem: there exists an integer \( N \) such that any number from a certain point on can be written as the sum of at most \( N \) prime numbers.
The Russian mathematician Vinogradov (1937) showed that any odd number from a certain point on can be written as the sum of 3 prime numbers.
The Chinese mathematician Chen (1966) showed that any sufficiently large even integer can be written as the sum of a prime number and another number that has at most two prime factors.
In 2013 the Peruvian mathematician Harald Helfgot published a possible proof of the weak conjecture. However, given the complexity of the proof, a revision of the mathematical community will be necessary before it can be accepted.
For an in-depth study of the additive theory of numbers see M. Nathanson’s book[10].
8) Applications to encryption
The problem of integer factorization has found important applications in the field of data encryption, fundamental with the great diffusion of the Internet. There are two main types of cryptographic algorithms:
- symmetric algorithms, that use the same key for encoding and decoding operations
- asymmetric algorithms, that use two different keys for the two operations
Symmetric algorithms require that both the sender and the recipient know the common key. This represents a fundamental limit for modern data transmission, which takes place through computer networks in all parts of the world.
Asymmetric algorithms provide two keys for each user: one public and one private. The public key can be registered in a public database accessible to all, while the private key must remain secret. The information encrypted with a public key can only be decoded with the associated private key.
The most famous symmetric encryption algorithm is the RSA algorithm, developed in 1977 by Ron Rivest, Adi Shamir and Leonard Adleman. The security of the RSA algorithm, on which public-key cryptography is based, relies on the difficulty of factoring whole numbers with a very large number of digits (> 200).
For an in-depth study of the link between Number Theory and Encryption see N. Koblitz’s book[11].
Conclusion
Number theory is the oldest branch of pure mathematics, and also the largest. There are still many unsolved problems, among which the most famous are Goldbach’s conjecture and Riemann’s hypothesis. However there are many other interesting problems concerning primes and their properties, relationships between numbers, sets of numbers with particular properties, configurations of particular sequences of numbers, etc. Many of these problems have an easy formulation but their solution is often very difficult or almost impossible.
Although such problems may appear unrelated to reality, they still attract the interest of many mathematicians. We can agree with the words of the great mathematician Jacobi (1804 – 1851): “The purpose of science is the honor of the human spirit and, from this point of view, a question of number theory is worth as much as one relating to the world system“.
Bibliography
[1]C. F. Gauss – Disquisitiones Arithmeticae (Springer-Verlag, 1985)
[2]Dickson – History of the Theory of Numbers, Vol. 1-2-3, (Chelsea Publishing Company, N.Y., 1971)
[3]Jay Goldman – The Queen of Mathematics (AK Peters, 1998)
[4]Niven, Zuckerman, Montgomery – An introduction to the Theory of Numbers, V edition (Wiley, 1991), pag. 20
[5]C. F. Gauss – Disquisitiones Arithmeticae (Springer-Verlag, 1985), pag. 396
[6]Hardy-Wright – An Introduction to the Theory of Numbers, V edition (Oxford, 1979), pag. 340-373
[7]T. Apostol – Introduction to Analytic Number Theory (Springer, 1976), pag. 278-290
[8]Edwards – Riemann’s Zeta Function (Academic Press, 1974)
[9]Titchmarsh – The Theory of the Riemann Zeta Function (Oxford Science Publications, 1996)
[10]M.Nathanson – Additive Number Theory (Springer GTM, 1996)
[11]N. Koblitz – A Course in Number Theory an Crytography (Springer GTM, 1994)

0 Comments