Problem
Suppose we have \( n \) numbers \(x_{1},x_{2}, \cdots x_{n} \), in that order. Compute the number \(C_{n} \) of ways of positioning the brackets to multiply the product of the \(n\) numbers, without changing the given order.
Hint
If \(n=2\) we have only one case: \((x_{1} x_{2})\)
If \(n=3\) we have the following cases: \(((x_{1} x_{2})x_{3}), (x_{1}(x_{2}x_{3}))\)
If \( n=4\) we have the following cases: \( (((x_{1}x_{2})x_{3})x_{4}) , ((x_{1}(x_{2}x_{3}))x_{4}) , ((x_{1}x_{2})(x_{3}x_{4})) \), \( (x_{1}((x_{2}x_{3})x_{4})) ,(x_{1}(x_{2}(x_{3}x_{4})))\)
It would also be useful to determine the recurrence equation for \(C_{n}\). It’s not difficult to prove that the recurrence equation is the following:
valid for \( n \ge 2 \). We have set the following initial conditions: \( C_{0}=0 \text { and } C_{1}=1\).
Solution 1
We can translate our problem into a similar problem of a well known random walk. Let’s look at the case \(n=4 \); we have the following possibilities:
\( (((x_{1}x_{2})x_{3})x_{4}) , ((x_{1}(x_{2}x_{3}))x_{4}) , ((x_{1}x_{2})(x_{3}x_{4})) \),
\( (x_{1}((x_{2}x_{3})x_{4})) , (x_{1}(x_{2}(x_{3}x_{4}))) \)
If we ignore the open parentheses, we note that in each string the number of closed parentheses is equal to \( n-1 \). Furthermore, the first element of a string is always a digit and the last one is a closed parenthesis. We can represent any string, for example \( ((x_{1}x_{2})(x_{3}x_{4})) \), ignoring the open parentheses, with the following diagram:
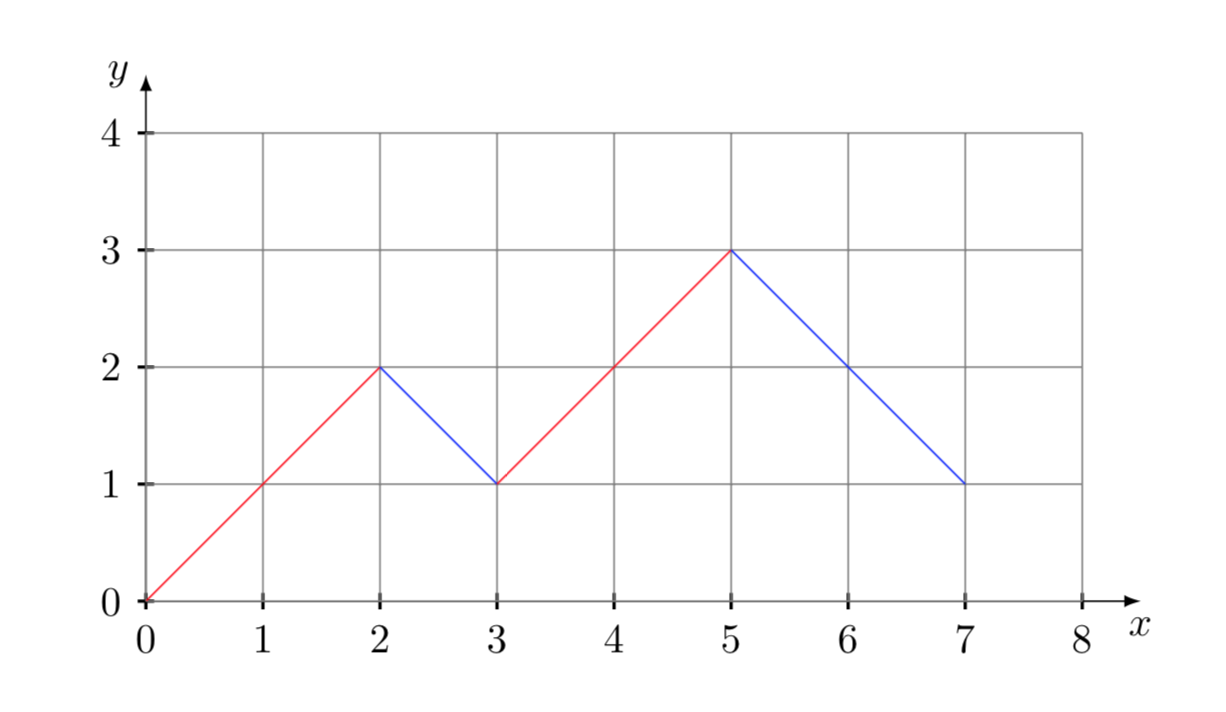
Every time we meet a digit we move upward, while if we encounter a closed parenthesis we move downward. The valid paths are those that, starting from the point of coordinates \( (0,0) \) do not touch or cross the x-axis, and terminate at the point of coordinates \( (2n-1,1) \). In fact, the problem is equivalent to counting the number of these paths. This is a classic problem of combinatorics and probability, widely known and solved. The number of paths to count is found by subtracting from the number of total paths the number of paths that touch or cross the x-axis. In general the total number of paths from the point \( (0,0) \) to the point \( (n, x) \) is equal to \( \displaystyle{\binom{n}{\frac{n+x}{2}}} \) . Applying this formula in our case we find that the total number of paths from the point \( (1,1) \) to the point \( (2n-1,1) \) is equal to
\[ T_{n} = \binom{2n – 2}{n-1} \\ \]To compute the number of paths, from the point \( (1,1) \) to the point \( (2n-1,1) \), that touch or cross the x-axis, we apply the reflection principle illustrated in the following diagram (see Feller, p. 72).
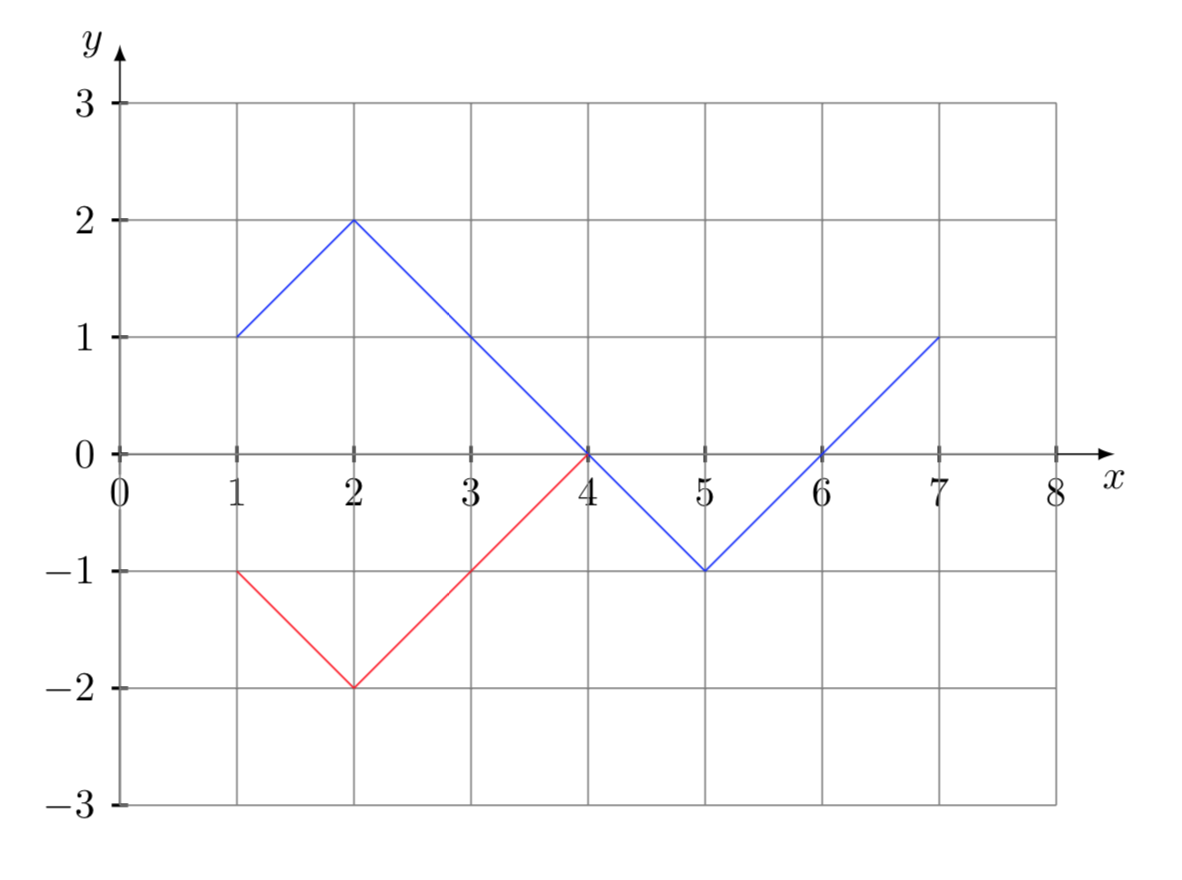
As can be clearly seen from the diagram, the number of paths, from the point \( (1,1)\) to the point \( (2n-1,1) \), touching or crossing the x-axis, indicated with \( S_{n} \), is equal to the total number of paths from the point \( (1, -1) \) to the point \( (2n-1,1) \). Therefore, applying the general formula described above, we have
\[ S_{n} = \binom{2n – 2}{n} \\ \]Making the difference we get the desired result:
\[ C_{n} = T_{n} – S_{n} = \frac{\binom{2n – 2}{n-1}}{n} \\ \]The numbers \( C_{n} \) are called Catalan numbers, in honor of the Belgian mathematician Catalan (1814–1894), and occur in many discrete mathematical problems.
Some books change the initial conditions and the Catalan number of order \( n\) is indicated with the value \( \displaystyle \frac{\binom{2n}{n}}{n+1} \), which corresponds to our \( C_{n+1} \).
For a discussion of these problems, see for example Feller[1] or Knuth[2].
Solution 2 (using generating functions)
Let \( F(x) \) be the generating function of the numbers \( C_{n} \):
\[ F(x) = C_{0} + C_{1}\cdot x + C_{2} \cdot x^2 + \cdots \\ \]If we compute the square of \( F(x) \) we have:
\[ F(x)^2 = C_{2} \cdot x^2 + C_{3} \cdot x^3 + \cdots \\ \]by virtue of the recurrence equation satisfied by the coefficients \( C_{n} \). With simple steps we can write the functional equation satisfied by the function \( F(x)\):
\[ F(x)^2 – F(x) + x = 0 \\ \]We solve this second degree equation in the variable \( F(x) \), treating \(x\) as a constant. Taking into account the initial conditions of the problem, one of the two solutions is discarded and the other is accepted:
\[ F(x) = \frac{1- \sqrt{1- 4 x}}{2} \\ \]At this point we find the Taylor series of this function, using use the general binomial theorem of Newton, valid for \( |x| < 1 \) and for every real number \( \alpha \):
\[ (1+x)^\alpha = 1 + \alpha x + \frac{\alpha \cdot (\alpha -1)x^2 }{2!}+ \frac{\alpha \cdot (\alpha -1)(\alpha -2)x^2}{3!}+ \cdots= \sum\limits_{k=0}^{\infty} \binom {\alpha}{k} x^k \\ \]Making the computations we finally find the solution:
\[ C_{n} = \frac{\binom{2n – 2}{n-1}}{n} \\ \]Bibliography
[1]William Feller – An introduction to Probability Theory and its applications, Vol. I (Wiley)
[2]Donald Knuth – The Art of Computer Programming, Vol. I – Fundamental Algorithms (Addison Wesley)

0 Comments