2
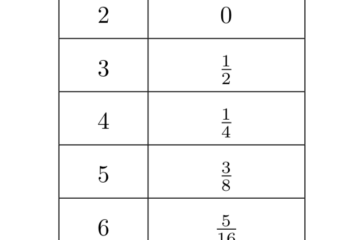
Problem Let \((a_{1},a_{2}, \cdots ,a_{n})\) be a permutation of the set \(\{1,2, \cdots,n \}\). Compute the average value, indicated with \(M_{n}\) , of the following sum: \[ (a_{1}- a_{2})^2 + (a_{2}-a_{3})^2 + \cdots + (a_{n-1} – a_{n})^2 \] taken on all permutations. If \(n=2\) the set of permutations is \(\{12,21\}\) Read more
Problem There are four people A, B, C, D. A box with a red ball inside it is given to A, who can leave things unchanged with probability \(p\) or replace the red ball with a white one with probability \(q=1-p\). The box is passed to B who can leave Read more
Problem Suppose we have \( n \) numbers \(x_{1},x_{2}, \cdots x_{n} \), in that order. Compute the number \(C_{n} \) of ways of positioning the brackets to multiply the product of the \(n\) numbers, without changing the given order. HintIf \(n=2\) we have only one case: \((x_{1} x_{2})\) If \(n=3\) Read more
Problem Suppose we compose numbers using only the digits in the set \( \{1,2,3\}\). Compute the total numbers with the following properties: having length \(n\) beginning and ending with the digit \(\displaystyle 1\) the adjacent digits are always different from each other We indicate this number with \(Z_{n}\). For example Read more
Problem Let’s consider the following \(5 \times 5\) matrix of positive integers: \[ \begin{pmatrix} d & 2d & 3d & ? & 5d \\ 11 & ? & ? & ? & ? \\ ? & 32 & ? & ? & ? \\ ? & ? & ? & Read more