The box principle is attributed to the German mathematician Dirichlet (1805-1859). It is also called the pigeonhole principle.
This article illustrates Dirichlet’s principle and gives a brief introduction to Ramsey’s theory, with some examples of computation of Ramsey numbers. For a deeper understanding of the topics of this article you can see [1].
1) Dirichlet’s box principle
Theorem 1.1 – Basic box principle
Let \(X \) be a set of \(n \) elements divided into \(r \) disjoint subsets. If \(n \gt r \) then at least one of the subsets contains more than one element.
Although it’s a very simple principle, it’s useful in many situations to solve even difficult problems.
Exercise 1.1
Let \(X = \{a_{1}, a_{2}, \cdots, a_{n} \} \) be a set of \(n\) integers. Prove that it’s always possible to choose a subset of \(X \) such that the sum of its numbers is divisible by \(n \).
Solution
Consider the following numbers: \(s_{1} = a_{1} \), \(s_{2} = a_{1} + a_{2} \), \(s_{n} = a_{1} + a_{2} + \cdots a_{n} \). Now, if any of the \(s_ {i} \) is divisible by \(n \) the problem is solved. Otherwise, dividing each sum by \(n \) the remainder can be \(\{1,2, \cdots (n-1) \} \). From this complete the proof, using the box principle.
Exercise 1.2
Given \(n + 1 \) integers, show that you can always choose two of them whose difference is divisible by \(n \).
Exercise 1.3
Let \(X\) be any set of \(r \) integers. If \(n \gt 1 \) and \(2^{r} \gt n + 1 \), prove that two distinct subsets of \(X \) can always be found such that the sums of their integers are congruent modulo \( n \), that is their difference is a multiple of \(n \).
Hint
Remember that given a set of \(r \) integers, the total number of non-empty subsets is \(2^{r} -1 \).
The condition \(2^{r} \gt n + 1 \) cannot be lowered. If \(2^{r} = n + 1 \) there is at least one set for which the property is no longer true. For example \(X = \{1,2,2^{2}, 2^{3}, \cdots 2^{r-1} \} \).
Exercise 1.4
Suppose we have a regular hexagon with a side equal to \(1 \). If there are \(7 \) points inside the surface of the hexagon, then there are at least two points whose distance is less than or equal to \(1 \).
Exercise 1.5
There are \(8 \) people sitting on an octagonal table. In each place there is a card with a person’s name (the names are all different). At first, all people sit in the wrong place. Prove that it’s always possible to rotate the table so that at least two people are in the right place.
Solution
For each person sitting around the table we calculate the distance from the card with his name, assuming a direction of rotation, counterclockwise for example. Possible values are \(\{1,2,3,4,5,6,7 \} \), since initially people were sitting in the wrong place. We can therefore apply the box principle: there are \(8 \) people and \(7 \) possible values of distances. For the box principle two persons must be at the same distance from their card. By making a rotation equal to this distance, the two persons will find themselves in front of their card.
Exercise 1.6
Consider the lattice of points with integer coordinates defined in the Cartesian plane. Prove that given any \(5 \) points of the lattice, the intermediate point of at least one pair is part of the lattice.
The intermediate point is defined by making the arithmetic averages of the coordinates of the two points.
2) The generalized box principle
Theorem 2.1
Suppose we have a set \(X \) of \(n\) objects, with \(n \gt mk \). If the set is divided into \(k \) disjoint subsets, then at least one of the subsets contains more than \(m \) elements.
Proof
Suppose \(X\) is partitioned into \(k\) disjoint sets:
Then, if it were \(| X_{i} | \le m, \forall i: 1\le i \le k \), we would have:
\[ n = | X | = \sum_{i = 1}^ {k} | X_{i} | \le mk \]contrary to the hypothesis that \(| X | = n \gt mk \).
Exercise 2.1
Show that, in a group of \(6\) people, at least \(3\) know each other or at least \(3\) don’t know each other.
Proof
Suppose that the \(6 \) people sit at the vertices of a hexagonal table. For each of the 15 pairs we draw a segment and assign a color: red if the people of the pair know each other, blue otherwise. From the geometric point of view, we have to prove that whatever colouring we make it’s always possible to find a triangle with only red sides or with only blue sides.
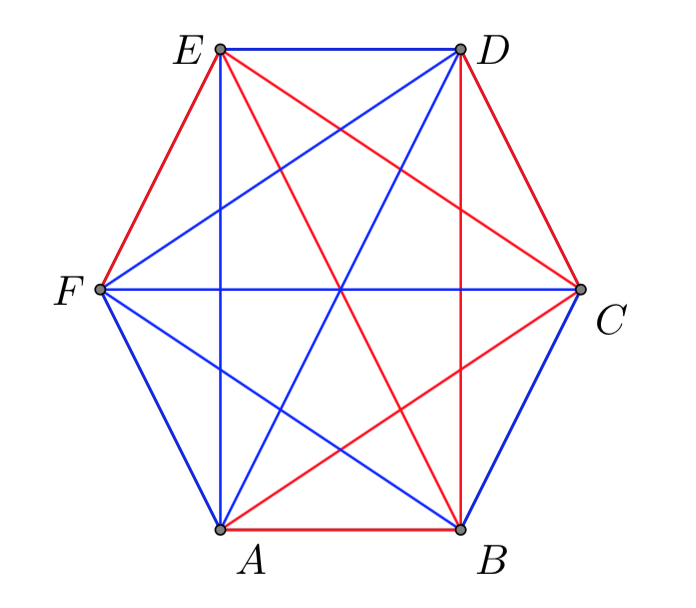
We choose any person in the group, denoting it with P. There are \(5\) people left; for Dirichlet’s principle two cases are possible:
- P knows at least three people
- at least three people don’t know P
Suppose the first case (the second is treated in a similar way). We denote the three people with A, B, C, and we draw red segments between P and A, B, C. Now, if there is a red segment between two people among A, B, C we are done; for example, if there is a segment between A and C we have the red triangle ACP. If the segments between A, B, C are all blue instead, we have the blue triangle ABC then.
3) Ramsey theory
Ramsey theory studies the properties that remain preserved in a partition of a given set. An equivalent way to define it is the following: if a set \(X \) has a given property \(P \) and is then decomposed into subsets, at least one of these retains the property \(P \) (“There is no complete disorder“).
To introduce Ramsey theory it’s necessary to remember some definitions on graphs and on the coloring of graphs.
3.1) Graphs and coloring
Definition 3.1
A graph is an ordered pair \(G = (V, E) \), where \(V \) is the set of elements called vertices or nodes and \(E \) is made up of a subset of the Cartesian product \(V \times V \), that is a set of pairs of vertices. The elements of \(E \) are called edges or arcs.
A graph is called simple if it has no loops, i.e. edges that start and end on the same vertex, or multiple edges between two vertices. The order of a graph is the number of vertices, i.e. the elements of \(V\). The degree of a vertex is the number of edges that are incident to the vertex. Two edges are called adjacent if they have a common vertex. Two vertices are called adjacent if there is an edge connecting them.
A graph is called directed if the pairs of vertices are ordered, otherwise it’s called undirected. In this article we only consider undirected graphs.
Definition 3.2
An undirected graph with \(n \) vertices is said to be complete, and is denoted with \(K_ {n} \), if each vertex is adjacent to all the other vertices.
Some examples are as follows:
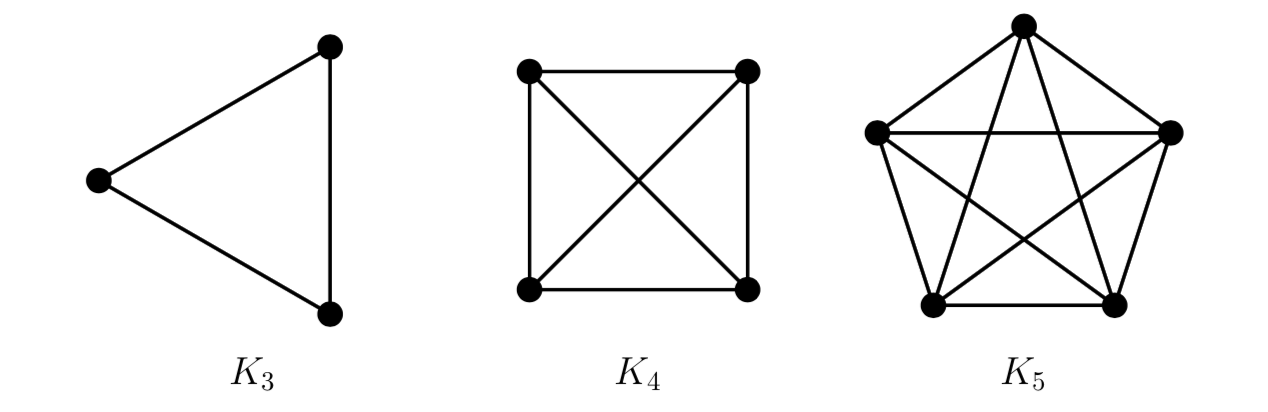
Exercise 3.1
Prove that the number of edges of a complete graph of order \(n \) is
Exercise 3.2
Prove that in an undirected graph \(G\) the sum of degrees of the vertices is equal to twice the number of the edges. Furthermore, the number of vertices of odd degree is even.
Definition 3.2
An r-coloring of the vertices of the graph \(G=(V, E) \) is a function \(f: V \to \{1,2, \cdots r \} \). The definition is similar for the r-coloring of the edges.
4) Ramsey’s theorem and Ramsey numbers
Ramsey theory is concerned in particular with the 2-coloring of the edges of a graph. By convention the colors red and blue are used.
Definition 4.1
Let \(s, t \) be two positive integers. The Ramsey number \(R (s, t) \) is defined as the order of the smallest complete graph which, if colored with two colors red and blue, contains a complete red-colored subgraph \(K_{s} \), or a complete blue-colored subgraph \(K_{t} \).
We give Ramsey’s basic theorem for two colors:
Theorem 4.1 – Ramsey
Given two positive integers \(s, t \), there exists a minimum integer \(n \), dependent on \(s, t \) and denoted with \(n = R(s, t) \), such that each 2-coloring of the arcs of a complete graph \(K_{n} \) of order \(n\), contains a complete subgraph of order \(s \), whose edges are all red, or contains a complete subgraph of order \(t \), whose edges are all blue.
Furthermore, if \(s, t \ge 2 \) then the following relation holds:
Ramsey’s basic theorem guarantees the existence of the number \(R (s, t) \) for each pair of positive integers \(s, t \). In a subsequent article we will illustrate in detail the theorem, with some of its extensions and applications. For a deeper study of Ramsey theory see [2].
Exercise 4.1
Prove the following relationships:
Exercise 4.2
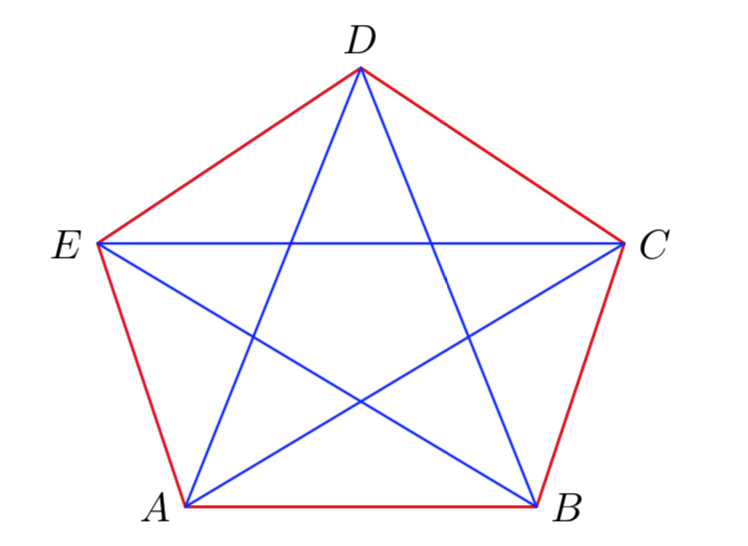
Prove that \(R (3,3) = 6 \). In other words, prove that for the complete graph \(K_{6} \) any coloring of the arcs with two colors red and blue, contains at least one triangle with all red or all blue sides.
Also, show that for a graph \(K_{5} \) you can always find a coloration that doesn’t contain any triangle with sides of the same color.
By exercise 2.1 we already know that \(K (3,3) \le 6 \). It remains to be shown that \(K (3,3) \gt 5 \). For this it’s sufficient to analyze the coloring of the following complete graph \(K_{5}\).
Exercise 4.3
Prove that each coloring with two colors of a complete graph \(K_{6} \) contains at least two monochrome triangles.
Solution
We already know that there is at least one monochromatic triangle, let’s say red, with three vertices \(v_{1}, v_{2}, v_{3} \). If the triangle \(v_{4}, v_{5}, v_{6} \) is also red, we are done. Otherwise, we assume that the arc \((v_{4}, v_{5}) \) is blue. We can exclude that between the arcs from \(v_{4}\) to the vertices \(v_{1}, v_{2}, v_{3} \) there are two red ones, otherwise we’ll have another red triangle. So there are two blue arcs. The same goes for the arcs \(v_{5} \) to the vertices \(v_{1}, v_{2}, v_{3} \). So, by the Dirichlet principle there must be a blue arc from \(v_{4} \) and a blue arc from \(v_{5} \), both of which go to the same vertex, among the three \(v_{1}, v_{2}, v_{3} \), forming a blue triangle.
Exercise 4.4
Prove that \(R (3,4) = 9\).
Hint
First we prove that \(R (3,4) \gt 8 \). For this the following figure is sufficient: it illustrates a coloring case of a graph \(K_{8} \) which does not contain a red graph \(K_{3} \) and not even a \(K_{4} \) blue.
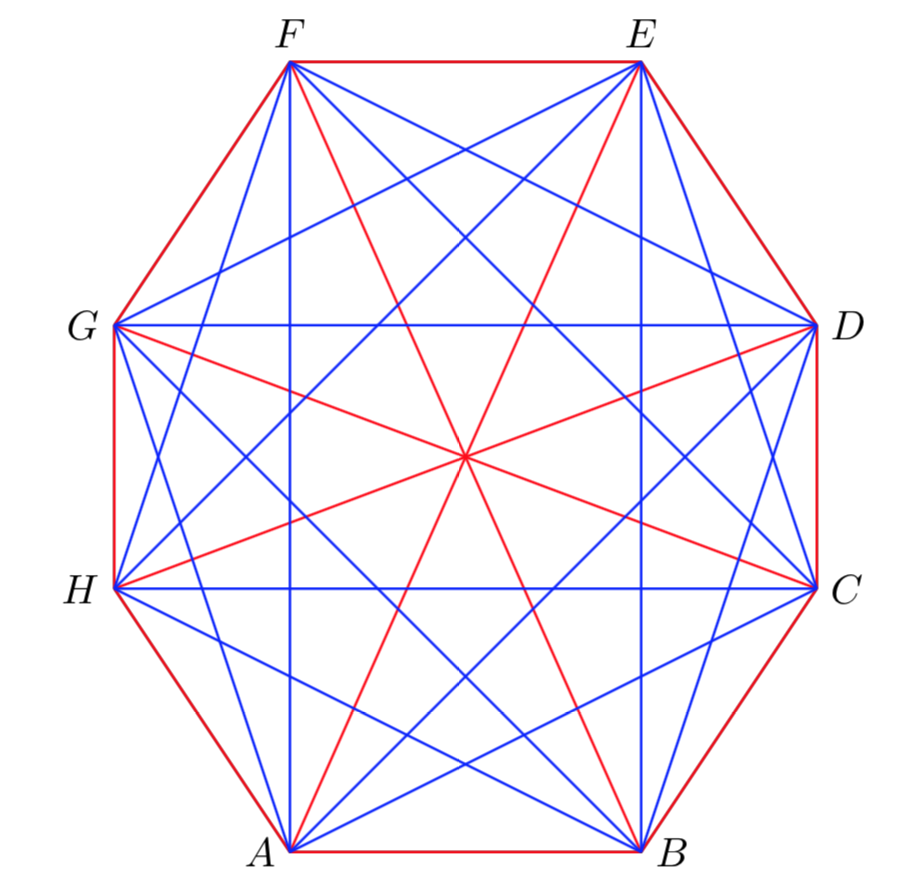
To prove that \(R (3,4) \le 9 \) applying Ramsey’s theorem we have: \(R (3,4) \le R (3,3) + R (2,4) = 6 + 4 = 10\).
It remains to be shown that \(R (3,4) \lt 10\). Suppose that there is a red and blue coloring of \(K_{9}\) such that there is no red subgraph \(K_{3}\) and no blue subgraph \(K_{4}\). Then each vertex of the graph must be incident with \(3\) red arcs and \(5\) blue arcs, otherwise it would be possible to build a red \(K_{3}\), or a blue \(K_{4}\), contrary to the hypothesis. Let us now consider only the red subgraph, which has \(9 \) vertices, each with three incident edges; the sum of the degrees of all the vertices is therefore \(3 \cdot 9 = 27\). This is not possible because the sum of the degrees of an undirected graph must be even (see Exercise 3.2). So the initial hypothesis is wrong and we can conclude that \(R (3,4) = 9\).
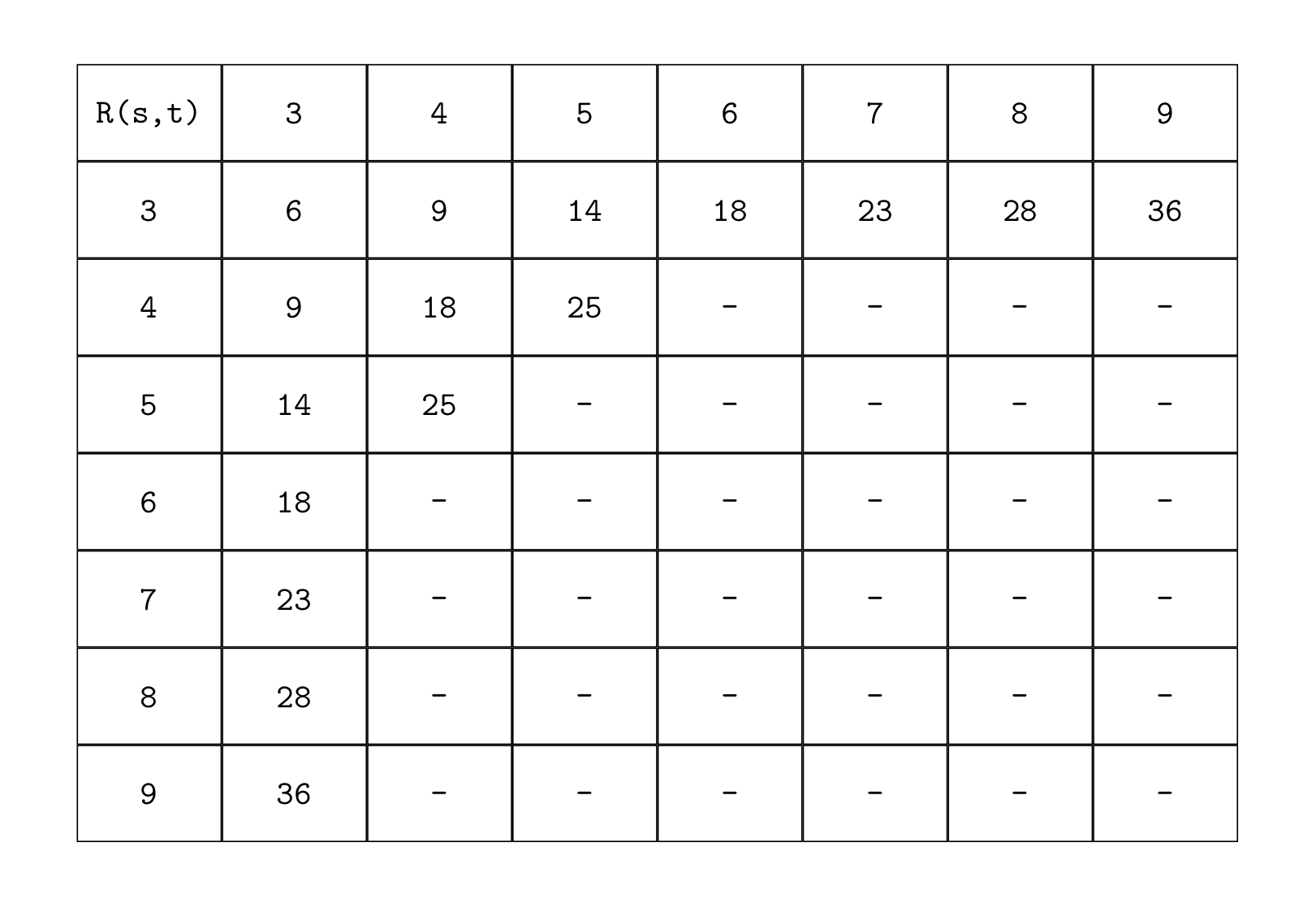
5) Computation of Ramsey numbers
The values of the Ramsey numbers are very difficult to calculate. Some of the calculated numbers are presented in the following table:
Conclusion
Ramsey’s theory finds interesting applications in various sectors, including number theory, algebra, information theory. In a future article we will describe Ramsey’s theory in more detail, with particular regard to applications to number theory.
Bibliography
[1]M. Erickson – Introduction to Combinatorics (Wiley)
[2]Graham, Rothschild, Spencer – Ramsey Theory (Wiley)

0 Comments